
Вышла книга автора сайта!
Теоретическая валидизация в социологическом исследовании: Методология и методы
Кривая нормального распределения и ее основные свойства
Кривая нормального распределения >> Распределение выборочных статистик
Многие являения и процессы окружающей действительности подчиняются нормальному закону. Например, ты с очень выской вероятностью имеешь средние умственные способности... ну, плюс-минус стандартное отклонение.

Дембицкий С. Кривая нормального распределения и ее основные свойства [Электронный ресурс]. - Режим доступа: http://www.soc-research.info/quantitative/1.html
Прежде чем говорить о конкретных методах сбора и анализа количественных данных, необходимо рассмотреть основные принципы, лежащие в основе количественного подхода в целом. К ним относится: а) использование свойств нормального распределения (или же других распределений: хи-квадрат, Фишера, Стьюдента и др.); б) использование особенностей распределения выборочных статистик; в) учет случайных ошибок, возникающих в любом выборочном исследовании.
Любому изучаемому свойству соответствует свое распределение в генеральной совокупности. Очень часто оно является нормальным и характеризуется двумя параметрами - средним значением и стандартным отклонением. Только эти два значения отличают друг от друга бесконечное множество нормальных кривых. Среднее задает положение кривой на числовой оси и выступает как некоторая исходная, нормативная величина измерения. Стандартное отклонение задает ширину этой кривой, зависит от единиц измерения и выступает как масштаб измерения.
Кривая нормального распределения (далее – КНР) – это теоретическая модель, представляющая собой абсолютно симметричное и гладкое распределение частот. Она имеет форму колокола и одну вершину, а ее концы уходят в бесконечность в обоих направлениях.
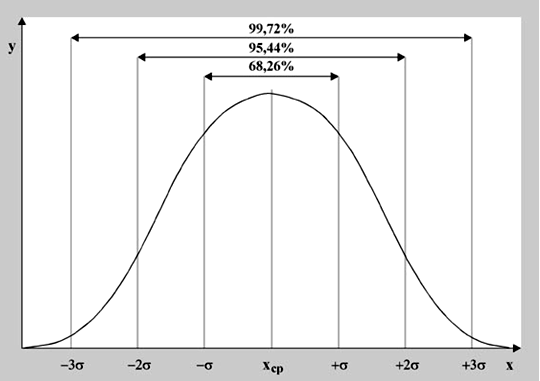
Главнейшим свойством КНР является то, что расстояние по абсциссе распределения (горизонтальная ось), измеренная в единицах стандартного отклонения от среднего арифметического распределения, всегда дает одинаковую общую площадь под кривой: между ±1 стандартным отклонением находится 68,26% площади, между ±2 стандартными отклонениями – 95,44% площади, между ±3 стандартными отклонениями – 99,72% площади.
Фактически, площадь в данном случае эквивалентна количеству человек в генеральной совокупности, которые имеют соответствующие параметры.
Любому изучаемому свойству соответствует свое распределение в генеральной совокупности. Очень часто оно является нормальным и характеризуется двумя параметрами - средним значением и стандартным отклонением. Только эти два значения отличают друг от друга бесконечное множество нормальных кривых. Среднее задает положение кривой на числовой оси и выступает как некоторая исходная, нормативная величина измерения. Стандартное отклонение задает ширину этой кривой, зависит от единиц измерения и выступает как масштаб измерения.
Кривая нормального распределения (далее – КНР) – это теоретическая модель, представляющая собой абсолютно симметричное и гладкое распределение частот. Она имеет форму колокола и одну вершину, а ее концы уходят в бесконечность в обоих направлениях.
Главнейшим свойством КНР является то, что расстояние по абсциссе распределения (горизонтальная ось), измеренная в единицах стандартного отклонения от среднего арифметического распределения, всегда дает одинаковую общую площадь под кривой: между ±1 стандартным отклонением находится 68,26% площади, между ±2 стандартными отклонениями – 95,44% площади, между ±3 стандартными отклонениями – 99,72% площади.
Фактически, площадь в данном случае эквивалентна количеству человек в генеральной совокупности, которые имеют соответствующие параметры.
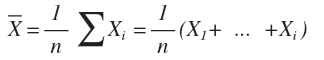
где Σ(Хі) – сума значений наблюдений, n – количество наблюдений.
Найдем среднее арифметическое для количества часов, которое Иван Петров тратил на сон на протяжении последней недели каждый день. Поскольку в неделе семь дней, то n = 7. Хі - это Х1 = 7 часов (понедельник), Х2 = 7 часов (вторник), Х3 = 6 часов (среда), Х4 = 7 часов (четверг), Х5 = 6 часов (пятница), Х6 = 9 часов (суббота), Х7 = 10 часов (воскресение).
Соответственно:
Найдем среднее арифметическое для количества часов, которое Иван Петров тратил на сон на протяжении последней недели каждый день. Поскольку в неделе семь дней, то n = 7. Хі - это Х1 = 7 часов (понедельник), Х2 = 7 часов (вторник), Х3 = 6 часов (среда), Х4 = 7 часов (четверг), Х5 = 6 часов (пятница), Х6 = 9 часов (суббота), Х7 = 10 часов (воскресение).
Соответственно:
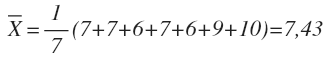
Стандартное отклонение является одной из наиблее часто используемых мер разбросах (мер, характеризующих неоднородность распределения). Если бы в нашем гипотетическом примере про Ивана Петрова, он каждый день спал по 8 часов, то от одного дня к другому никакой неоднородности не наблюдалось бы. В таком случае стандартное отклонение было бы равно 0 (полная однородность распределения).
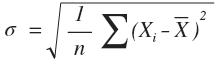
В нашем случае стандартное отклонение будет равно (условия см. в предыдущем примере):
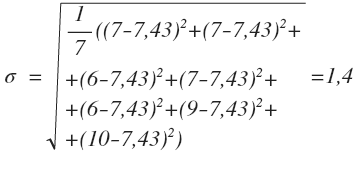
Несмотря на то, что ни одно из эмпирических распределений не имеет формы, которая бы точно отвечала этой идеальной модели, многие из них достаточно близки к ней, что разрешает сделать предположение об их нормальности. В свою очередь, это предположение позволяет использовать КНР и ее свойства для того, чтобы проанализировать соответствующие эмпирические распределения.
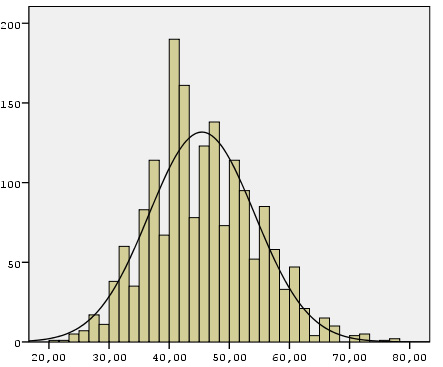
Выше приведено эмпирическое распределение для такой психологической характеристики как тревожность среди респондентов (n = 1725), отображающих население Украины (опрос был проведен в 2008 году). На графике изображено как эмпирическое распределение или фактически полученные ответы (столбцы от 20 до 80, где меньшие значения соответствуют меньшей тревожности, а большие – большей), так и идеальная модель нормального распределения (колоколоподобная кривая).
Как видно из приведенного графика эмпирическое распределение не совпадает на 100% с идеальной моделью КНР. Тем не менее, эмпирическое распределение достаточно близко к нормальному, что позволяет использовать свойства последнего. Так, зная, что среднее значение для тревожности респондентов приблизительно равно 45, а стандартное отклонение – 9, можно сделать вывод, что 68,26% всего населения Украины имеет социальное самочувствие от 36 до 54 пунктов. Из-за ошибок измерения эта информация носит приблизительных характер, но все равно достаточно близка к истинным величинам.
Как видно из приведенного графика эмпирическое распределение не совпадает на 100% с идеальной моделью КНР. Тем не менее, эмпирическое распределение достаточно близко к нормальному, что позволяет использовать свойства последнего. Так, зная, что среднее значение для тревожности респондентов приблизительно равно 45, а стандартное отклонение – 9, можно сделать вывод, что 68,26% всего населения Украины имеет социальное самочувствие от 36 до 54 пунктов. Из-за ошибок измерения эта информация носит приблизительных характер, но все равно достаточно близка к истинным величинам.
- default_titleХили Дж. Статистика. Социологические и маркетинговые исследования. - К.: ООО "ДиаСофтЮП"; СПб.: Питер, 2005. - 638 с.
- default_titleНаследов А. Математические методы психологического исследования. - СПб.: Речь, 2004. - 392 с.
- Show More