
Вышла книга автора сайта!
Теоретическая валидизация в социологическом исследовании: Методология и методы
Анализ парных связей
Описание взаимосвязей между явлениями и процессами - отдельная тема. Поэтому предлагаю поговорить о ней более подробно.

Дембицкий С. Анализ парных связей [Электронный ресурс]. - Режим доступа: http://www.soc-research.info/quantitative/6-1.html
Согласно исследованию научных публикаций в наиболее престижных зарубежных журналах, посвященных социальным и поведенческим наукам (Ч.Теддли, М.Элайс, 2010), 77% всех социологических исследований проведены в рамках количественного подхода. Из них 71% является корреляционными исследованиями или исследованиями, посвященными изучению связей между социальными явлениями.
Самый простой вид корреляционных исследований - изучение парных взаимосвязей или совместной изменчивости двух переменных. Такого рода исследования пригодны для решения двух научных задач:
Самый простой вид корреляционных исследований - изучение парных взаимосвязей или совместной изменчивости двух переменных. Такого рода исследования пригодны для решения двух научных задач:
а) доказательства существования причинно-следственной связи между переменными (наличие связи является важным, но не единственным, условием причинно-следственной зависимости); б) предсказания: в случае наличия связи между переменными можно с определенным уровнем точности предсказывать значения одной переменной, если нам известно значение другой.
Связь между двумя переменными есть в том случае, когда изменение категории одной переменной ведет к изменению распределения второй:
Связь между двумя переменными есть в том случае, когда изменение категории одной переменной ведет к изменению распределения второй:
Продуктивность труда |
Удовлетворенность работой |
Вместе |
||
Низкая |
Средняя |
Высокая |
||
Низкая |
30 |
21 |
7 |
58 |
Средняя |
20 |
25 |
18 |
63 |
Высокая |
10 |
15 |
27 |
52 |
Вместе |
60 |
61 |
52 |
173 |
Продуктивность труда |
Удовлетворенность работой |
||
Низкая |
Средняя |
Высокая |
|
Низкая |
50,0% |
34,4% |
13,5% |
Средняя |
33,3% |
41,0% |
34,6% |
Высокая |
16,7% |
24,6% |
51,9% |
Вместе |
100% |
100% |
100% |
Легко заметить, что в зависимости от категории переменной "Удовлетворенность работой" переменная "Продуктивность труда" меняет свое распределение. Следовательно, мы можем сделать вывод о существовании связи между переменными.
Также из этого примера видно, что каждому из значений одной переменной отвечает несколько значений другой. Такие связи называются статистическими или вероятностными. В данном случае, связь между переменными не является абсолютной. В нашем случае это означает, что кроме удовлетворенности работой есть и другие факторы, влияющие на продуктивность труда.
В случае же, когда одному значению первой переменной соответствует лишь одно значение второй, говорят о функциональных связях. Вместе с тем, даже когда есть основания говорить о функциональной связи, невозможно на все 100% продемонстрировать ее в эмпирической действительности по двум причинам: а) из-за погрешности измерительных инструментов; б) из-за невозможности контроля всех условий окружающей среды, влияющих на эту связь. И поскольку в социальных науках ученые имеют дело именно с вероятностными связями, постольку ниже речь пойдет именно о них.
Парные связи владеют тремя характеристиками: силой, направлением и формой.
Сила показывает насколько согласованна изменчивость двух переменных. Сила связи может изменяться в диапазоне от 0 до +1 (если хотя бы одна из переменных относится к номинальной шкале) или от -1 до +1 (если обе переменные относятся, по крайней мере, к порядковой шкале). При этом 0 и близкие к ней величины говорят об отсутствии связи между переменными, а величины близкие к +1 (прямая связь) или -1 (обратная связь) - о сильной связи. Один из вариантов интерпретации связи, с точки зрения ее силы, выглядит следующим образом:
Также из этого примера видно, что каждому из значений одной переменной отвечает несколько значений другой. Такие связи называются статистическими или вероятностными. В данном случае, связь между переменными не является абсолютной. В нашем случае это означает, что кроме удовлетворенности работой есть и другие факторы, влияющие на продуктивность труда.
В случае же, когда одному значению первой переменной соответствует лишь одно значение второй, говорят о функциональных связях. Вместе с тем, даже когда есть основания говорить о функциональной связи, невозможно на все 100% продемонстрировать ее в эмпирической действительности по двум причинам: а) из-за погрешности измерительных инструментов; б) из-за невозможности контроля всех условий окружающей среды, влияющих на эту связь. И поскольку в социальных науках ученые имеют дело именно с вероятностными связями, постольку ниже речь пойдет именно о них.
Парные связи владеют тремя характеристиками: силой, направлением и формой.
Сила показывает насколько согласованна изменчивость двух переменных. Сила связи может изменяться в диапазоне от 0 до +1 (если хотя бы одна из переменных относится к номинальной шкале) или от -1 до +1 (если обе переменные относятся, по крайней мере, к порядковой шкале). При этом 0 и близкие к ней величины говорят об отсутствии связи между переменными, а величины близкие к +1 (прямая связь) или -1 (обратная связь) - о сильной связи. Один из вариантов интерпретации связи, с точки зрения ее силы, выглядит следующим образом:
Значение |
Интерпретация |
до |0,2| |
очень слабая связь |
до |0,5| |
слабая связь |
до |0,7| |
средняя связь |
до |0,9| |
сильная связь |
свыше |0,9| |
очень сильная связь |
Все значения в таблице приведены в модуле, т.е. должны анализироваться безотносительно к знаку. Так, например, связь -0,67 и +0,67 являются одинаковыми по силе, но разными по направлению.
Сила связи определяется с помощью коэффициентов корреляции. К коэффициентам корреляции относятся, например, фи и V-крамера (номинальные переменные, мало категорий/табличный вид), Гамма (порядковые переменные, мало категорий/табличный вид), Кендалла и Спирмена (порядковые переменные, много категорий), Пирсона (метрические переменные, много категорий).
Направление говорит о характере взаимного изменения категорий переменных. Если с увеличением значений одной переменной значения другой переменной также увеличиваются, то связь является прямой (или положительной). Если же ситуация противоположная и увеличение значений одной переменной ведет к уменьшению значений второй, то связь обратная (или отрицательная).
Направление связи может иметь место только в тех случаях, когда речи идет о порядковых и/или метрических переменных, то есть тех переменных, значения которых можно упорядочить от меньших к большим или наоборот. Таким образом, если хотя бы одна переменная относится к номинальной шкале, то можно говорить только о силе связи и ее форме, но не о направлении.
Сила связи определяется с помощью коэффициентов корреляции. К коэффициентам корреляции относятся, например, фи и V-крамера (номинальные переменные, мало категорий/табличный вид), Гамма (порядковые переменные, мало категорий/табличный вид), Кендалла и Спирмена (порядковые переменные, много категорий), Пирсона (метрические переменные, много категорий).
Направление говорит о характере взаимного изменения категорий переменных. Если с увеличением значений одной переменной значения другой переменной также увеличиваются, то связь является прямой (или положительной). Если же ситуация противоположная и увеличение значений одной переменной ведет к уменьшению значений второй, то связь обратная (или отрицательная).
Направление связи может иметь место только в тех случаях, когда речи идет о порядковых и/или метрических переменных, то есть тех переменных, значения которых можно упорядочить от меньших к большим или наоборот. Таким образом, если хотя бы одна переменная относится к номинальной шкале, то можно говорить только о силе связи и ее форме, но не о направлении.
Направление связи можно определить либо с помощью таблиц сопряженности (мало категорий), либо с помощью диаграммы рассеяния (много категорий), либо с помощью знака коэффициента корреляции (количество категорий переменных не имеет значения):
Пример положительной связи
2-я перем-я |
1-я перем-я |
||
Кат.А |
Кат.В |
Кат.С |
|
Кат.А |
50% |
30% |
20% |
Кат.В |
30% |
40% |
20% |
Кат.С |
20% |
30% |
60% |
∑ |
100% |
100% |
100% |
Пример отрицательной связи
Для правильной интерпретации связи с помощью таблиц необходимо их правильное оформление. Так, в нашем случае, категория А является наименьшим значением в случае обоих переменных, а категория С - наибольшим.
2-я перем-я |
1-я перем-я |
||
Кат.А |
Кат.В |
Кат.С |
|
Кат.А |
10% |
30% |
75% |
Кат.В |
20% |
40% |
15% |
Кат.С |
70% |
30% |
10% |
∑ |
100% |
100% |
100% |
В данной диаграмме представлена взаимосвязь между количеством усилий, которые прикладывают студенты в процессе учебы (10-бальная порядковая шкала, ось Х), и успешностью их учебы в бакалаврате (среднее значение успешности сдачи сессий за 4 года обучения, ось Y). Поскольку нижний левый угол соответствует малым значениям обоих переменных, а верхний правый - большим, постольку диаграмма свидетельствует о положительной взаимосвязи между переменными. Думаю, вы представляете, как бы выглядела диаграмма рассеяния в случае отрицательной взаимосвязи.
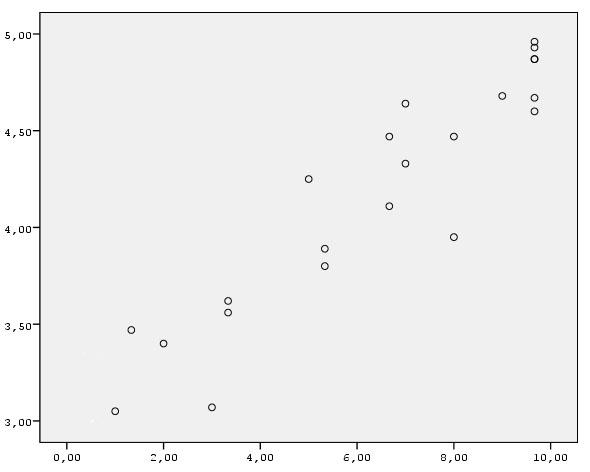
В результате подсчета коэффициент корреляции равен либо положительному, либо отрицательному значению, что само по себе говорит о его направлении.
Несмотря на то, что значения коэффициента корреляции достаточно для получения основной информации про связь между переменными, его вычисление принято предварять построением таблицы или диаграммы рассеяния, которые необходимы для получения дополнительной информации, в частности - про форму связи.
Несмотря на то, что значения коэффициента корреляции достаточно для получения основной информации про связь между переменными, его вычисление принято предварять построением таблицы или диаграммы рассеяния, которые необходимы для получения дополнительной информации, в частности - про форму связи.
Форма связи указывает на особенности совместной изменчивости двух переменных. В зависимости от того, к какой шкале относится переменная, форму связи можно проанализировать либо с помощью столбчатой диаграммы/таблицы сопряженности (если хотя бы одна переменная является номинальной), либо с помощью диаграммы рассеяния (для порядковых и метрических шкал).
Обратимся к примеру. В одном из своих исследования, единицами анализа которого выступили две кафедры разных вузов, я установил, что сила связи между переменными равна 0,83 в обоих случаях (в качестве переменных выступили тип студента и успешность сдачи последней сессии). Таким образом, сила и направление связи были одинаковы для обоих вузов. В свою очередь форма связи показала важные отличия (нажмите на график для увеличения):
Обратимся к примеру. В одном из своих исследования, единицами анализа которого выступили две кафедры разных вузов, я установил, что сила связи между переменными равна 0,83 в обоих случаях (в качестве переменных выступили тип студента и успешность сдачи последней сессии). Таким образом, сила и направление связи были одинаковы для обоих вузов. В свою очередь форма связи показала важные отличия (нажмите на график для увеличения):
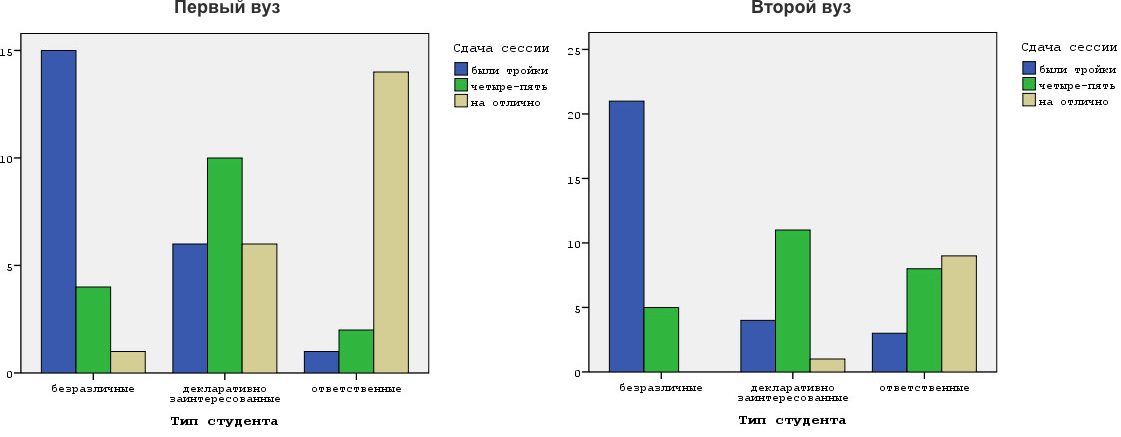
Различия в форме распределения очевидны. Судя по всему, на первой кафедре значительно легче учиться, чем на второй. На это, в частности, указывает количество студентов, сдавших сессию на отлично.
Диаграммы рассеяния дают более ценную в аналитическом смысле информацию - кроме сравнения различных единиц анализа, они позволяют оценить отклонение связи от линейности. Линейность является важным условием эффективного применения коэффициентов корреляции и многих других статистических методов. Она наблюдается в том случае, когда каждое новое увеличение значений одной из переменных на единицу ведет к увеличению значений другой переменной на одинаковую или приблизительно одинаковую величину. Так, для приведенной ранее диаграммы рассеяния, увеличение значения 10-бальной шкалы на единицу ведет к увеличению успешности студента на величину близкую к 0,2.
Когда связь между переменными достаточно близка к идеальной линейной модели, коэффициенты корреляции адекватно отображают силу связи и ее направление (в случае представленной ранее диаграммы рассеяния, сила связи равна 0,93). В противном случае (т.е. в случае нелинейных связей) необходимо использовать специальные методы анализа данных. Примером диаграммы, демонстрирующей криволинейную связь, может служить следующий:
Диаграммы рассеяния дают более ценную в аналитическом смысле информацию - кроме сравнения различных единиц анализа, они позволяют оценить отклонение связи от линейности. Линейность является важным условием эффективного применения коэффициентов корреляции и многих других статистических методов. Она наблюдается в том случае, когда каждое новое увеличение значений одной из переменных на единицу ведет к увеличению значений другой переменной на одинаковую или приблизительно одинаковую величину. Так, для приведенной ранее диаграммы рассеяния, увеличение значения 10-бальной шкалы на единицу ведет к увеличению успешности студента на величину близкую к 0,2.
Когда связь между переменными достаточно близка к идеальной линейной модели, коэффициенты корреляции адекватно отображают силу связи и ее направление (в случае представленной ранее диаграммы рассеяния, сила связи равна 0,93). В противном случае (т.е. в случае нелинейных связей) необходимо использовать специальные методы анализа данных. Примером диаграммы, демонстрирующей криволинейную связь, может служить следующий:
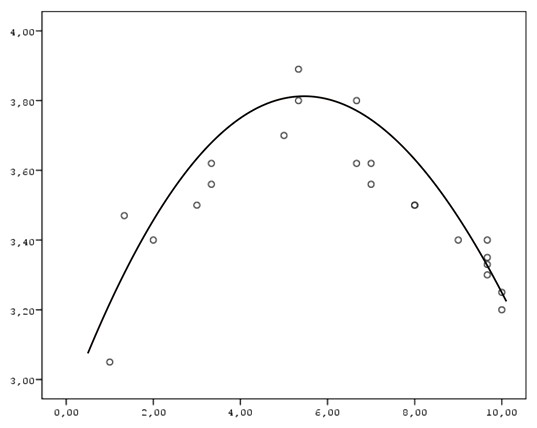
Такая форма связи может быть, например, между тревожностью студента и успешностью сдачи экзамена, когда как чрезмерно низкая, так и чрезмерно высокая тревожность приводят к снижению успешности.
Подводя итог, хочется отметить один важный момент: анализ связи с точки зрения ее силы, направления и формы - это только первый шаг анализа парных связей. После того, как мы определили что взаимосвязь представляет научный или практический интерес, необходимо проверить ее на статистическую значимость, так как наличие связи в выборке еще не означает ее наличие в генеральной совокупности. Такого рода задачи решаются с помощью методов статистического вывода, специфика которых рассмотрена далее.
Подводя итог, хочется отметить один важный момент: анализ связи с точки зрения ее силы, направления и формы - это только первый шаг анализа парных связей. После того, как мы определили что взаимосвязь представляет научный или практический интерес, необходимо проверить ее на статистическую значимость, так как наличие связи в выборке еще не означает ее наличие в генеральной совокупности. Такого рода задачи решаются с помощью методов статистического вывода, специфика которых рассмотрена далее.
- default_titleХили Дж. Статистика. Социологические и маркетинговые исследования. - К.: ООО "ДиаСофтЮП"; СПб.: Питер, 2005. - 638 с.
- default_titleБююль А., Цефель П. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. - СПб.: ООО "ДиаСофтЮП", 2005. - 608 с.
- Show More