Информация, полученная из выборки, привязывается к генеральной совокупности путем механизма, который носит название распределения выборочных статистик. Распределение выборочных статистик (далее – РВС) – это теоретическое распределение вероятностей статистик (под статистиками может пониматься, например, среднее значение той или иной характеристики) для всех возможных выборок заданного объема. Таким образом, РВС включает значение всех статистик, отвечающих каждой возможной комбинации заданного размера выборки. Наиболее важным свойством РВС является то, что его характеристики основаны на законах теории вероятности, а не на эмпирической информации.
Пример:
Допустим генеральная совокупность состоит всего из 16 человек, а выборка которую мы хотим извлечь – из 3 человек. Параметр подлежащий оценке – среднее количество комнат в квартирах респондентов. Предположим, что в генеральной совокупности 4 человека имеет 1 комнату, 4 человека – 2 комнаты, 4 человека – 3 комнаты, 4 человека – 4 комнаты. Такое распределение называется равномерным и выглядит в данном случае следующим образом:

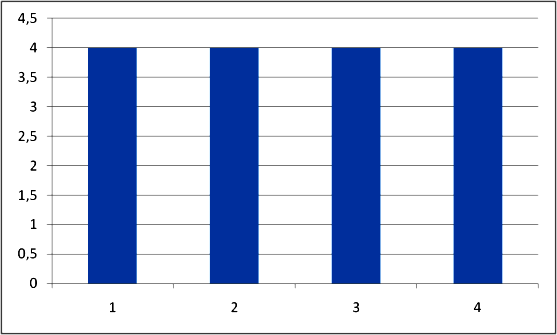
Соответственно первый респондент, отобранный в выборку, может иметь одно-, двух-, трех- или четырехкомнатную квартиру. Тоже самое справедливо для второго и третьего респондентов. Зная это и используя правила сложения и умножения вероятностей мы можем вычислить вероятность формирования того или иного варианта выборки.

Правило сложения вероятностей: вероятность осуществления того или иного случайного события из некоторого множества несовместных случайных событий равна сумме их вероятностей.
Правило умножения вероятностей: вероятность одновременного осуществления любого числа случайных событий равна произведению их индивидуальных вероятностей.
Для более детального ознакомления с этими правилами рекомендую можно обратиться, например, к книге Грегори Кимбла "Как правильно пользоваться статистикой".

Во-первых, рассчитаем вероятность получения трех базовых выборок: А) все три респондента будут иметь одинаковое количество комнат; Б) два респондента имеют одинаковое количество комнат, а третий не такое как первые два; В) все три респондента имеют разное количество комнат.
Вариант А = 4/16 * 3/15 * 2/14 = 24/3360 или 0,7%;
Вариант Б = 4/16 * 3/15 * 4/14 = 48/3360 или 1,4%;
Вариант В = 4/16 * 4/15 * 4/14 = 64/3360 или 1,9%.
Во-вторых рассмотрим все возможное комбинации выборок размером три человека для указанной генеральной совокупности. При этом разные варианты выборок сгруппированы в зависимости от среднего значения комнат (Xcp.), которое они показывают.

Зная вероятность выпадения базовых выборок (все из представленных комбинаций подпадают под один из трех вариантов), а также имея количество комбинаций, отвечающих каждому из возможных средних значений, можно рассчитать вероятность получения того или иного среднего значения в результате формирования выборки из трех человек.
В качестве примера рассчитаем вероятность получения выборки, которая бы давала среднее значение равное 2 (№4 в табл.). В данной группе встречается одна выборка варианта А (2+2+2), три выборки варианта Б (1+1+4, 1+4+1, 4+1+1) и шесть выборок варианта В (2+1+3, 2+3+1, 1+3+2, 1+2+3, 3+2+1, 3+1+2). Теперь, исходя из вероятности формирования каждого из вариантов, можно получить итоговое значение вероятности получения Xcp. = 2:
1*вероятность получения варианта А + 3*вероятность получения варианта Б + 6*вероятность получения варианта В = 0,7%*1 + 1,4%*3 + 1,9*6 = 0,7% + 4,2% + 11,4% = 16,3% (на самом деле 16,4%, одна десятая процента потеряна в результате операции округления).
Таким же образом можно рассчитать вероятность получения всех остальных средних значений для выборки в три человека. Если же на основе соответствующей информации построить график, то получится следующее:

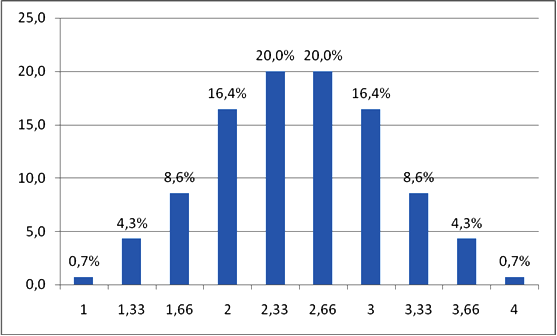
Как вы можете видеть, приведенное распределение очень близко к нормальному. Это важный момент, который для данного РВС выражен в центральной предельной теореме: если из генеральной совокупности, имеющей любое распределение со средним µ и стандартным отклонением s, многократно извлекать случайные выборки объемом n, то при большом n (не менее 100 наблюдений) распределение всех возможных выборочных средних будет стремиться к нормальному распределению со средним µ и стандартным отклонением s/√n.
Если конкретизировать эту теорему для нашего случая, то очевидно, что получение выборки, среднее значение которой близко к истинному среднему значению (для нашей генеральной совокупности из 16 человек µ = 2,5), намного выше, чем вероятность получения выборки, значение которой далеко от среднего генеральной совокупности. Так, вероятность того, что мы получим выборку, среднее значение которой минимально отклоняется от истинного (на 0,17 или 0,16 пунктов), составляет 40%. В свою очередь, вероятность того, что мы получим выборку, среднее значение которой отклоняется от истинного значения не более чем на 0,5 пунктов, составляет 72,8%. Соответственно вероятность получения выборки, среднее значение которой отличается от истинного более чем на 0,5 пункта составляет 27,2%.
Конечно же, приведенный пример не в полной мере соответствует условиям центральной предельной теоремы по причине малого объема как генеральной совокупности, так и выборки. Вместе с тем, он хорошо демонстрирует специфику РВС и особенности ее свойств для простой случайной выборки.
Есть и другие случаи РВС, отличные от нормального распределения (например, распределения Стьюдента, Фишера, хи-квадрат и другие). Вместе с тем принцип их использования носит схожий характер – они позволяют оценить вероятность определенных событий и на этой основе сделать научные выводы.