
Вышла книга автора сайта!
Теоретическая валидизация в социологическом исследовании: Методология и методы
Виды статистических методов: статистические выводы
Описательная статистика >> Статистические выводы > Величина интервальных оценок | Непараметрические критерии
Вот то, чем мы гордимся - наши выводы, никогда не лишенные вероятности ошибки! Пусть последнее тебя не пугает, обычно вероятность ошибиться ничтожно мала.

Дембицкий С. Виды статистических методов: статистические выводы [Электронный ресурс]. - Режим доступа: http://www.soc-research.info/quantitative/7.html
Как было сказано ранее, статистические выводы используются для обобщения данных из выборки в отношении всей генеральной совокупности. Случайные ошибки, характерные для выборочного исследования, могут привести к тому, что выборка не будет [достаточно точной] моделью генеральной совокупности. В действительности выборка никогда не является моделью генеральной совокупности на все 100%, а лишь ее более или менее искаженным вариантом. Для того, чтобы оценить такие искажения и, следовательно, сделать более точные выводы о генеральной совокупности и используются статистические выводы.
Прежде всего, они позволяют оценить вероятность того, что выявленные в выборке взаимосвязи, различия, величины и т.д. характерны исключительно для выборки, но не для генеральной совокупности. Логика здесь следующая: если такая вероятность высока, то принимается решение, согласно которому параметры выборки не характерны для генеральной совокупности и наоборот – если такая вероятность низка, то принято считать, что соответствующие параметры выборки говорят о параметрах генеральной совокупности.
Прежде всего, они позволяют оценить вероятность того, что выявленные в выборке взаимосвязи, различия, величины и т.д. характерны исключительно для выборки, но не для генеральной совокупности. Логика здесь следующая: если такая вероятность высока, то принимается решение, согласно которому параметры выборки не характерны для генеральной совокупности и наоборот – если такая вероятность низка, то принято считать, что соответствующие параметры выборки говорят о параметрах генеральной совокупности.
Важно помнить – достижение 100% гарантии того, что результаты, полученные в исследовании, характерны для генеральной совокупности, возможно лишь в том случае, когда проведено сплошное исследование, т.е. опрос всех представителей генеральной совокупности. Но это уже не выборочное исследование и оно не предполагает использование статистических выводов.
В самом общем виде статистические выводы можно разделить на две группы: 1) интервальное оценивание (построение интервала, в который с заданной вероятностью должно попасть среднее значение либо пропорция генеральной совокупности); 2) проверка статистических гипотез (вероятностный вывод о том, что определенные параметры выборочной совокупности отображают (или же нет) параметры генеральной совокупности).
Для того, чтобы рассмотреть каждую из групп, нажмите на соответствующую кнопку ниже.
В самом общем виде статистические выводы можно разделить на две группы: 1) интервальное оценивание (построение интервала, в который с заданной вероятностью должно попасть среднее значение либо пропорция генеральной совокупности); 2) проверка статистических гипотез (вероятностный вывод о том, что определенные параметры выборочной совокупности отображают (или же нет) параметры генеральной совокупности).
Для того, чтобы рассмотреть каждую из групп, нажмите на соответствующую кнопку ниже.
Интервальное оценивание
Во многих случаях бывает необходимо на основе единичного параментра выборки (среднее значение или пропорция) оценить соответствующий параметр генеральной совокупности. Если выборка достаточна большая (100 и более наблюдений), используя свойства кривой нормального распределения, а также центральную придельную теорему, можно построить интервал, в который с заданной вероятностью попадет истинное значение.
Как вы помните из второй главы, распределение выборочных средних имеет нормальный вид. Соответственно вероятность получения выборки со средним близким к среднему значению генеральной совокупности весьма высока. Но даже в тех случаях, когда среднее для выборки будет достаточно сильно отличаться от среднего генеральной совокупности, доверительный интервал [в подавляющем большинстве случаев] будет включать истинное значение. И лишь в очень редких случаях будут получены выборки с настолько сильно отличающимися параметрами выборки и генеральной совокупности, что истинное значение не попадет в доверительный интервал.
Мы не станем детальнее углубляться в соответствующие доказательства и примеры, а просто рассмотрим технику построения доверительных интервалов.
Доверительные интервалы для средних значений
Во многих случаях бывает необходимо на основе единичного параментра выборки (среднее значение или пропорция) оценить соответствующий параметр генеральной совокупности. Если выборка достаточна большая (100 и более наблюдений), используя свойства кривой нормального распределения, а также центральную придельную теорему, можно построить интервал, в который с заданной вероятностью попадет истинное значение.
Как вы помните из второй главы, распределение выборочных средних имеет нормальный вид. Соответственно вероятность получения выборки со средним близким к среднему значению генеральной совокупности весьма высока. Но даже в тех случаях, когда среднее для выборки будет достаточно сильно отличаться от среднего генеральной совокупности, доверительный интервал [в подавляющем большинстве случаев] будет включать истинное значение. И лишь в очень редких случаях будут получены выборки с настолько сильно отличающимися параметрами выборки и генеральной совокупности, что истинное значение не попадет в доверительный интервал.
Мы не станем детальнее углубляться в соответствующие доказательства и примеры, а просто рассмотрим технику построения доверительных интервалов.
Доверительные интервалы для средних значений
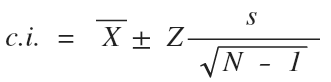
где Z - стандартизированное значение, определяемое уровнем альфа или p-значением (вероятностью того, что истинное значение не попадет в доверительный интервал);
s - стандартное отклонение по выборке;
n - размер выборки.
Очевидно что s и n известны нам из самого исследования. В свою очередь, Z определяется с помощью таблицы стандартизированных значений:
s - стандартное отклонение по выборке;
n - размер выборки.
Очевидно что s и n известны нам из самого исследования. В свою очередь, Z определяется с помощью таблицы стандартизированных значений:
Доверительный уровень |
Альфа (р) |
Z-значение |
90% |
0,10 |
±1,65 |
95% |
0,05 |
±1,96 |
99% |
0,01 |
±2,58 |
99,9% |
0,001 |
±3,29 |
Доверительный уровень говорит о том, с какой вероятностью истинное значение попадет в построенный интервал.
Рассмотрим пример. Допустим из выборки (n = 300) известно, что среднее значение для месячного заработка киевлян составляет 4000 грн., а стандартное отклонение - 75 грн. Если нас удовлетворит вероятность ошибки равная 5% (альфа - 0,05), то Z = ±1,96.
Рассмотрим пример. Допустим из выборки (n = 300) известно, что среднее значение для месячного заработка киевлян составляет 4000 грн., а стандартное отклонение - 75 грн. Если нас удовлетворит вероятность ошибки равная 5% (альфа - 0,05), то Z = ±1,96.
Отсюда:
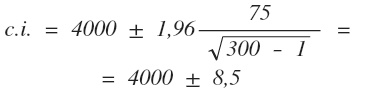
Таким образом, истинное значение для киевлян с вероятностью 95% должно попасть в интервал от 3991,5 грн. до 4008,5 грн.
Доверительные интервалы для пропорций
Доверительные интервалы для пропорций
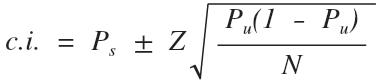
По сравнению с предыдущей, в данной формуле остался размер выборки и Z-значение. Последнее определяется оно также с помощью приведенной выше таблицы.
Другие составляющие следующие:
Ps - значение пропорции для выборки;
Pu - значение пропорции для генеральной совокупности.
У наиболее внимательных из вас мог возникнуть вопрос: откуда мы возьмем Pu, если мы хотим использовать Ps для его оценки? Или: если нам известно Pu, то зачем нам Ps? Действительно, Ps нам только и нужно для того, чтобы оценить неизвестное Pu. Выход из этой ситуации достаточно простой - за Pu принимают такую величину (как вы помните для пропорций оно может варьироваться от 0 до 1), которая бы дала нам наибольшее значение выражения Pu(1-Pu). В таком случае и сам доверительный интервал примет наибольшее значение (при прочих равных условиях). Фактически исследователь должен пойти на заведомое увеличение интервала, ведь больший интервал с большей вероятностью будет включать искомую истинную величину для генеральной совокупности. Таким значением является 0,5:
0,5(1-0,5) = 0,5*0,5 = 0,25
Теперь рассмотрим пример. Пусть, согласно результатам предвыборного опроса, за оппозиционную партию готово проголосовать 17% населения (Ps = 0,17), размер выборки составляет 1200 человек, а уровень альфа - 0,01. Тогда:
Другие составляющие следующие:
Ps - значение пропорции для выборки;
Pu - значение пропорции для генеральной совокупности.
У наиболее внимательных из вас мог возникнуть вопрос: откуда мы возьмем Pu, если мы хотим использовать Ps для его оценки? Или: если нам известно Pu, то зачем нам Ps? Действительно, Ps нам только и нужно для того, чтобы оценить неизвестное Pu. Выход из этой ситуации достаточно простой - за Pu принимают такую величину (как вы помните для пропорций оно может варьироваться от 0 до 1), которая бы дала нам наибольшее значение выражения Pu(1-Pu). В таком случае и сам доверительный интервал примет наибольшее значение (при прочих равных условиях). Фактически исследователь должен пойти на заведомое увеличение интервала, ведь больший интервал с большей вероятностью будет включать искомую истинную величину для генеральной совокупности. Таким значением является 0,5:
0,5(1-0,5) = 0,5*0,5 = 0,25
Теперь рассмотрим пример. Пусть, согласно результатам предвыборного опроса, за оппозиционную партию готово проголосовать 17% населения (Ps = 0,17), размер выборки составляет 1200 человек, а уровень альфа - 0,01. Тогда:
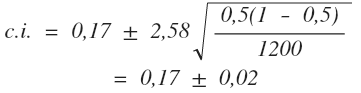
Следовательно с вероятностью в 99% за оппозиционную партию проголосует от 15% до 19% населения.
- default_titleХили Дж. Статистика. Социологические и маркетинговые исследования. - К.: ООО "ДиаСофтЮП"; СПб.: Питер, 2005. - 638 с.
- default_titleМалхотра Н. Маркетинговые исследования. - М: Вильямс, 2007. - 1200 с.
- default_titleField A. Discovering statistics using SPSS. - London, Thousand Oaks, New Delhi: Sage, 2009. - 822 p.
- Show More
Проверка статистических гипотез.
В процессе проверки статистических гипотез исследователь на основании полученных данных проверяет гипотезу, согласно которой все выявленные взаимосвязи между явлениями или различия между группами являются результатом случайных ошибок.
Проверка статистических гипотез состоит из следующих этапов: 1) Проверка допущений. 2) Формулировка статистических гипотез. 3) Определение уровня альфа (p-значения). 4) Расчет эмпирического значения критерия и количества степеней свободы. 5) Использование теоретического распределения: определение критического значения и его сопоставление с эмпирическим значением. Рассмотрим основы проверки статистических гипотез на примере критерия независимости хи-квадрат. Этот критерий позволяет на основании данных таблицы сопряженности проверить есть ли взаимосвязь между двумя переменными. Он является непараметрическим, т.е. таким критерием, который не требует проверки допущений о форме распределения выборочных статистик.
В процессе проверки статистических гипотез исследователь на основании полученных данных проверяет гипотезу, согласно которой все выявленные взаимосвязи между явлениями или различия между группами являются результатом случайных ошибок.
Проверка статистических гипотез состоит из следующих этапов: 1) Проверка допущений. 2) Формулировка статистических гипотез. 3) Определение уровня альфа (p-значения). 4) Расчет эмпирического значения критерия и количества степеней свободы. 5) Использование теоретического распределения: определение критического значения и его сопоставление с эмпирическим значением. Рассмотрим основы проверки статистических гипотез на примере критерия независимости хи-квадрат. Этот критерий позволяет на основании данных таблицы сопряженности проверить есть ли взаимосвязь между двумя переменными. Он является непараметрическим, т.е. таким критерием, который не требует проверки допущений о форме распределения выборочных статистик.
Этап 1. Для использования критерия хи-квадрат, данные должны удовлетворять всего двум допущениям: а) Используются независимые случайные выборки. Независимые выборки имеют место в том случае, когда отбор респондентов в одну выборку никак не влияет на отбор респондентов в другую.
Во-первых, эти данные должны быть получены от студентов, отобранных случайным образом (например, с помощью случайного отбора из общего списка студентов того или иного вуза). В таком случае, выборки будут также и независимыми - не важно, кто был отобран последним, далее может быть отобран любой парень или девушка, еще не попавшие в выборку.
б) Переменные относятся к номинальной шкалы. А поскольку номинальные шкалы являются наиболее "слабыми", использование порядковых и метрических переменных также возможно (после того, как количество их категорий будет уменьшино до необходимого количества).
Во-первых, эти данные должны быть получены от студентов, отобранных случайным образом (например, с помощью случайного отбора из общего списка студентов того или иного вуза). В таком случае, выборки будут также и независимыми - не важно, кто был отобран последним, далее может быть отобран любой парень или девушка, еще не попавшие в выборку.
б) Переменные относятся к номинальной шкалы. А поскольку номинальные шкалы являются наиболее "слабыми", использование порядковых и метрических переменных также возможно (после того, как количество их категорий будет уменьшино до необходимого количества).
Для примера обратимся к представленной ниже таблице, с помощью которой проверяется влияние пола студентов на успешность их обучения:
Зеленым цветом обозначены маргинальные частоты по строкам и столбцам. Они понадобятся в дальнейшем для расчета ожидаемых частот.
| Успешность | Пол |
Вместе
|
|
Женский |
Мужской |
||
| Были тройки | 16 |
12 |
28 |
| Четыре-пять | 20 |
4 |
24 |
| На отлично | 10 |
0 |
10 |
| Вместе | 46 |
16 |
62 |
Этап 2. Статистические гипотезы делятся на два вида - нулевую и альтернативную. В зависимости от статистического метода, нулевая гипотеза утверждает либо отсутствие различий между группами (при сравнении средних значений или пропорций), либо отстуствие связи между переменными. В свою очередь, альтернативная гипотеза утверждает обратное нулевой - наличие различий или наличие связи.
Все эти утверждения имеют отношение именно к генеральной совокупности, так как выявленные в выборке связи между переменными или различия между группами могут быть вызваны случайными ошибками и не иметь отношения к генеральной совокупности. В нашем случае нулевая гипотеза будет утверждать отсутствие связи между полом студентов и их успешностью, альтернативная - наличие таковой.
Этап 3. Обычно величина альфа должна быть 0,05 или менее. Тогда наш вывод, основанный на примененении статистического критерия, будет верным с вероятностью 95% или выше.
Этап 4. Эмпирическое значение статистического критерия - это специальное значение, вычисленное на основании имеющихся данных с использованием того или иного теоретического распределения. Эмпирическое значение позволяет оценить вероятность того, что выборочные данные были получены в результате случайных ошибок. Для подавляющего большинства методов проверки статистических гипотез большие эмпирические значения с большей вероятностью указывают именно на существование связей или различий (т.е. на слабое влияние случайных ошибок выборки).
Этап 3. Обычно величина альфа должна быть 0,05 или менее. Тогда наш вывод, основанный на примененении статистического критерия, будет верным с вероятностью 95% или выше.
Этап 4. Эмпирическое значение статистического критерия - это специальное значение, вычисленное на основании имеющихся данных с использованием того или иного теоретического распределения. Эмпирическое значение позволяет оценить вероятность того, что выборочные данные были получены в результате случайных ошибок. Для подавляющего большинства методов проверки статистических гипотез большие эмпирические значения с большей вероятностью указывают именно на существование связей или различий (т.е. на слабое влияние случайных ошибок выборки).
В случае хи-квадрат, прежде чем перейти к расчету эмпирического значения, необходимо рассчитать ожидаемые частоты (fe) в ячейках, характерные для ситуации полного отстуствия связи между переменными, а потом сравнить их с имеющимися частотами (fo). Для этого по каждой ячейке необходимо умножить маргинальную частоту по столбцу на маргинальную частосту по строке и разделить на общее количество наблюдений:
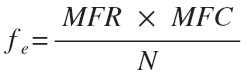
где MFR - маргинальная частота по строке, MFC - маргинальная частота по столбцу, N - общее количество наблюдений.
Для нашего примера расчет ожидаемых частот будет иметь следующий вид:
Для нашего примера расчет ожидаемых частот будет иметь следующий вид:
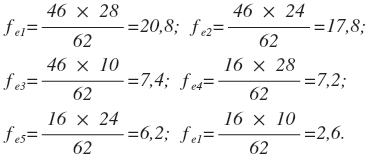
Соответственно таблица с теоретическим распределением, для которого характерно полное отсутствие связи между переменными будет выглядеть так:
| Успешность | Пол |
Вместе
|
|
Женский |
Мужской |
||
| Были тройки | 20,8 |
7,2 |
28 |
| Четыре-пять | 17,8 |
6,2 |
24 |
| На отлично | 7,4 |
2,6 |
10 |
| Вместе | 46 |
16 |
62 |
Если различия между этими частотами и частотами, полученными в процессе исследования, достаточно велики, будет принята альтернативная гипотеза, если же нет - нулевая.
Определение величины различий осуществляется с помощью специального показателя, который и является эмпирическим (или же экспериментальным) значением критерия:
Определение величины различий осуществляется с помощью специального показателя, который и является эмпирическим (или же экспериментальным) значением критерия:
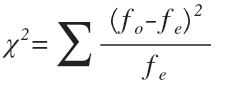
Для нашего случая эмпирическое значение критерия будет равно:
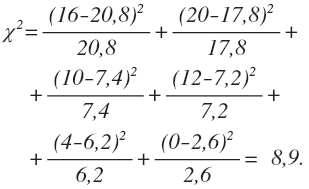
Кроме эмпирического значения большинство методов проверки статистических гипотез предполагает расчет количества степеней свободы (df), которое используется при определении критического значения, то есть той величины, с которой необходимо сравнить эмпирическое значение. Именно такое сравнение позволяет оценить достаточно ли велико эмпирическое значение (оно должно превышать критическое) для того, чтобы отказаться от нулевой гипотезы и принять альтернативную.
Для хи-квадрат df = (r-1)(c-1), где r - количество строк в таблице, а c - количество столбцов. Соответственно, в нашем случае df = (3-1)(2-1) = 2.
Этап 5. Все методы проверки статистических гипотез предполагают использование тех или иных распределений выборочных статистик, позволяющих определять критическое значение в каждом конкретном исследовании. Критическое значение, как и эмпирическое, является специальной величиной, которая задает некоторую границу, превышение которой говорит о том, что имеющиеся результаты с очень низкой вероятностью (эта вероятность равна величине альфа) могли быть получены вследствие случайных ошибок.
Этап 5. Все методы проверки статистических гипотез предполагают использование тех или иных распределений выборочных статистик, позволяющих определять критическое значение в каждом конкретном исследовании. Критическое значение, как и эмпирическое, является специальной величиной, которая задает некоторую границу, превышение которой говорит о том, что имеющиеся результаты с очень низкой вероятностью (эта вероятность равна величине альфа) могли быть получены вследствие случайных ошибок.
Распределение хи-квадрат, используемое для анализа таблиц сопряженности, меняет свой вид в зависимости от количества степеней свободы. Соответственно меняется и распределение критических значений (на рисунке df обозначается как k):
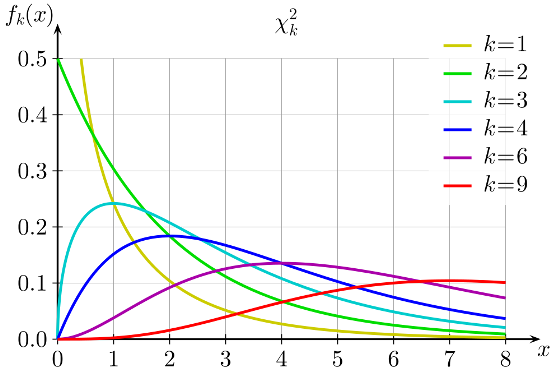
Само критическое значение в каждом конкретном случае определяются с помощью таблиц критических значений. В случае хи-квадрат такая таблица имеет два параметра - количество степеней свободы и уровень альфа.
После определения критического значения, его необходимо сравнить с эмпирическим - если критическое значение больше, принимается нулевая гипотеза (т.к. вероятность получения результата вследствие случайных ошибок слишком велика), если же эмпирическое значение больше, принимается альтернативная гипотеза.
Для нашего примера, альфа равное 0,05 и df равное 2, дают критическое значение равное 5,99. С учетом того, что эмпирическое значение больше критического (8,9 > 5,99), можно принять альтернативную гипотезу. При этом вероятность ошибочности такого решения составляет 5%.
Всегда важно помнить, что делая статистический вывод исследователь рискует сделать ошибку вне зависимости от того какую гипотезу он принял - нулевую или альтернативную. Такие ошибки называются статистическими и делятся на две группы - первого и второго рода. При ошибках первого рода на основании данных выборки принимается альтернативная гипотеза, в то время как для генеральной совокупности верна нулевая. Соответственно, при ошибке второго рода на основании данных выборки принимается нулевая гипотеза, в то время как для генеральной совокупности верна альтернативная.
После определения критического значения, его необходимо сравнить с эмпирическим - если критическое значение больше, принимается нулевая гипотеза (т.к. вероятность получения результата вследствие случайных ошибок слишком велика), если же эмпирическое значение больше, принимается альтернативная гипотеза.
Для нашего примера, альфа равное 0,05 и df равное 2, дают критическое значение равное 5,99. С учетом того, что эмпирическое значение больше критического (8,9 > 5,99), можно принять альтернативную гипотезу. При этом вероятность ошибочности такого решения составляет 5%.
Всегда важно помнить, что делая статистический вывод исследователь рискует сделать ошибку вне зависимости от того какую гипотезу он принял - нулевую или альтернативную. Такие ошибки называются статистическими и делятся на две группы - первого и второго рода. При ошибках первого рода на основании данных выборки принимается альтернативная гипотеза, в то время как для генеральной совокупности верна нулевая. Соответственно, при ошибке второго рода на основании данных выборки принимается нулевая гипотеза, в то время как для генеральной совокупности верна альтернативная.
- default_titleХили Дж. Статистика. Социологические и маркетинговые исследования. - К.: ООО "ДиаСофтЮП"; СПб.: Питер, 2005. - 638 с.
- default_titleМалхотра Н. Маркетинговые исследования. - М: Вильямс, 2007. - 1200 с.
- default_titleField A. Discovering statistics using SPSS. - London, Thousand Oaks, New Delhi: Sage, 2009. - 822 p.
- Show More

