
Вышла книга автора сайта!
Теоретическая валидизация в социологическом исследовании: Методология и методы
Виды статистических методов: описательная статистика
Анализ количественных данных начинается с описания. Соответствующие методы очень просты, но в то же время чрезвычайно информативны.

Дембицкий С. Виды статистических методов: описательная статистика [Электронный ресурс]. - Режим доступа: http://www.soc-research.info/quantitative/6.html
Согласно широко используемой типологии, статистические методы можно разделить на описательную статистику и статистические выводы. Описательная статистика используется для простого обобщения данных, полученных в рамках выборочного исследования. В свою очередь, статистические выводы необходимы для того, чтобы данные, полученные из выборки, можно было распространить на всю генеральную совокупность.
К базовым методам описательной статистики относятся процентные показатели, меры центральной тенденции, меры вариации и парные коэффициенты связи. Они позволяют обобщить данные, имеющиеся по выборке.
К базовым методам описательной статистики относятся процентные показатели, меры центральной тенденции, меры вариации и парные коэффициенты связи. Они позволяют обобщить данные, имеющиеся по выборке.
Процентные показатели используются для того, чтобы частотное распределение по той или иной переменной привести к основе 100 (аналогично, пропорции используются для приведения данных к основе 1). В таком виде данные являются более предпочтительными в интуитивном смысле по сравнению с «сырым» частотным распределением.
Пример (успешность сдачи сессии):
Пример (успешность сдачи сессии):
| Успешность | Частота |
% |
Пропорции |
| Были тройки | 28 |
45,2 |
0,452 |
| Без троек, в основном на четыре | 11 |
17,7 |
0,177 |
| Без троек, в основном на пять | 13 |
21,0 |
0,210 |
| На отлично | 10 |
16,1 |
0,161 |
| Вместе | 62 |
100,0 |
1,000 |
Меры центральной тенденции (мода, медиана и среднее арифметическое) дают информацию о типичном или центральном значении распределения. Мода говорит о наиболее часто встречающемся значении, медиана – о серединном значении, среднее арифметическое – о наиболее ожидаемом значении.
В приведенном выше примере модой будет вариант ответа «Были тройки», так как его отметило 28 человек – больше, чем любой другой вариант.
Для того чтобы найти медиану, необходимо упорядочить все варианты ответа по возрастанию или убыванию – сначала все варианты «Были тройки», потом все варианты «Без троек, в основном на четыре» и т.д. Если количество наблюдений нечетное, необходимо найти то значение, которое будет стоять посередине этого упорядоченного ряда. Оно и будет медианой. Если же количество наблюдений четное, надо взять два значения которые стоят посередине и найти их среднее значение. Поскольку в нашем случае 62 наблюдения, то посередине будет стоять 31 и 32 наблюдение. Это варианты «Без троек, в основном на четыре». Следовательно, медианой также будет значение «Без троек, в основном на четыре».
Как рассчитывается среднее арифметическое, показано в первой главе. В нашем случае, расчет среднего значения не совсем корректен. Но если мы присвоим вариантам ответов конкретные числовые значения (например, 1, 2, 3, 4), то сможем осуществить расчет среднего.
В приведенном выше примере модой будет вариант ответа «Были тройки», так как его отметило 28 человек – больше, чем любой другой вариант.
Для того чтобы найти медиану, необходимо упорядочить все варианты ответа по возрастанию или убыванию – сначала все варианты «Были тройки», потом все варианты «Без троек, в основном на четыре» и т.д. Если количество наблюдений нечетное, необходимо найти то значение, которое будет стоять посередине этого упорядоченного ряда. Оно и будет медианой. Если же количество наблюдений четное, надо взять два значения которые стоят посередине и найти их среднее значение. Поскольку в нашем случае 62 наблюдения, то посередине будет стоять 31 и 32 наблюдение. Это варианты «Без троек, в основном на четыре». Следовательно, медианой также будет значение «Без троек, в основном на четыре».
Как рассчитывается среднее арифметическое, показано в первой главе. В нашем случае, расчет среднего значения не совсем корректен. Но если мы присвоим вариантам ответов конкретные числовые значения (например, 1, 2, 3, 4), то сможем осуществить расчет среднего.
Меры вариативности говорят о степени неоднородности распределения (например, размах, коэффициент изменчивости категорий, стандартное отклонение и др.). Самым простым, как в смысле получаемой информации, так и в смысле подсчета, является размах (R). Он равен разнице между наибольшим и наименьшим значениями распределения. Например, если наименьший рост среди респондентов равен 147 сантиметров, а наибольший – 198, то размах будет равен 51 сантиметру.
Для количественных признаков нижняя граница мер изменчивости равна 0 (по интересующей исследователя характеристике наблюдаемые объекты не отличаются). В свою очередь, верхняя граница – всегда открытая величина, определяющаяся особенностями изучаемого свойства и наблюдаемой неоднородностью распределения. Например, стандартное отклонение для роста населения Украины в 2008 году было равно 9 сантиметрам (среднее равно 169 см), а для возраста – 17 лет (среднее равно 46 годам).
Поскольку расчет стандартного отклонения был рассмотрен ранее, здесь мы коснемся только коэффициента изменчивости категорий (IQV) – единственной меры вариативности, применение которой является полностью корректной в случаях номинальных и порядковых шкал. В данном случае коэффициент может изменяться в диапазоне от 0 (отсутствие изменчивости) до 1 (максимальная изменчивость).
Для количественных признаков нижняя граница мер изменчивости равна 0 (по интересующей исследователя характеристике наблюдаемые объекты не отличаются). В свою очередь, верхняя граница – всегда открытая величина, определяющаяся особенностями изучаемого свойства и наблюдаемой неоднородностью распределения. Например, стандартное отклонение для роста населения Украины в 2008 году было равно 9 сантиметрам (среднее равно 169 см), а для возраста – 17 лет (среднее равно 46 годам).
Поскольку расчет стандартного отклонения был рассмотрен ранее, здесь мы коснемся только коэффициента изменчивости категорий (IQV) – единственной меры вариативности, применение которой является полностью корректной в случаях номинальных и порядковых шкал. В данном случае коэффициент может изменяться в диапазоне от 0 (отсутствие изменчивости) до 1 (максимальная изменчивость).
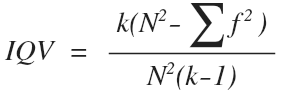
где k – количество категорий переменной, N – общее количество наблюдений в выборке, ∑f^2 – сумма квадратов частот.
Рассмотрим чему равно IQV для примера с успешностью студентов. Расчет этого коэффициента вручную удобно осуществлять с помощью специальной таблицы (впрочем, как и многих других статистик).
| Успешность | Частота |
Квадрат частоты |
| Были тройки | 28 |
784 |
| Без троек, в основном на четыре | 11 |
121 |
| Без троек, в основном на пять | 13 |
169 |
| На отлично | 10 |
100 |
| Вместе | N = 62 N^2 = 3844 |
∑f^2 = 1174 |
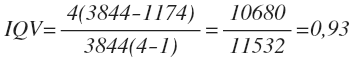
Парные коэффициенты связи предназначены для анализа силы и направления связей между переменными. В этот класс входит достаточно большое количество методов, которые можно разделить на две группы в зависимости от того, в каком виде представлены данные. Первая группа предназначена для анализа переменных, имеющих малое количество категорий и представленных в виде таблиц сопряженности (например, V-Крамера для номинальных переменных и Гамма для порядковых).
| Успешность | Пол |
Вместе |
|
Женский
|
Мужской |
||
| Были тройки | 16 |
12 |
28 |
| Четыре-пять | 20 |
4 |
24 |
| На отлично | 10 |
0 |
10 |
| Вместе | 46 |
16 |
62 |
Таблицы сопряженности предназначены для представления данных о связи между двумя переменными. Для улучшения информативности следует расчитать процентные величины в отдельности для каждого из столбцов. Для приведенного примера, соответствующая таблица будет выглядеть следующим образом:
| Успешность | Пол |
Вместе
|
|
Женский |
Мужской |
||
| Были тройки | 34,8% |
75,0% |
45,2% |
| Четыре-пять | 43,5% |
25,0% |
38,7% |
| На отлично | 21,7% |
0,0% |
16,1% |
| Вместе | 100,0% |
100,0% |
100,0% |
Вторая группа методов предназначена для ситуаций, когда переменные имеют большое количество категорий, для группировки которых не существует очевидных границ, либо же когда такая группировка может привести к потере части информации (например, коэффициенты корреляции Пирсона или Спирмена).
Расчет коэффициентов связи носит более сложный характер по сравнению с рассмотренными ранее методами. Для ознакомления с соответствующими формулами и их использованием лучше обратиться к специализированной литературе. На уровне описательной статистики, парные связи могут анализироваться в смысле силы связи, а также ее характера и/или направления.
Сила связи может варьироваться в интервале от 0 до 1 (если хотя бы одна переменная относится к номинальной шкале: например, связь между полом и успешностью обучения) или от –1 до +1 (если обе переменные относятся, хотя бы к порядковой шкале: например, связь между уровнем образования и уровнем заработка). Полное отсутствие связи соответствует 0, максимальная связь наблюдается как при –1, так и при +1. Максимальная сила связи является научной идеализацией. Соответственно, в реальной жизни значения соответствующих коэффициентов принимают промежуточные значения между –1 и 0 или 0 и +1. Например, сила связи между ростом и весом мужчин равна +0,38, для женщин этот показатель равен всего лишь +0,18 (Украина, 2008 год).
Знак связи говорит о ее направлении. Отрицательная связь указывает, что при увеличении значений одной переменной, значения другой будут уменьшаться. Если же связь положительная, то значения обоих переменных будут изменяться в одном направлении. Связь между ростом и весом, как вы понимаете, является положительной. Следовательно, более высокие люди с большей вероятностью будут иметь и больший вес. Отрицательной, например, будет связь между количеством выпитого за ночь алкоголя и самочувствием с утра.
Более подробно анализ связей рассмотрен в следующей главе.
Расчет коэффициентов связи носит более сложный характер по сравнению с рассмотренными ранее методами. Для ознакомления с соответствующими формулами и их использованием лучше обратиться к специализированной литературе. На уровне описательной статистики, парные связи могут анализироваться в смысле силы связи, а также ее характера и/или направления.
Сила связи может варьироваться в интервале от 0 до 1 (если хотя бы одна переменная относится к номинальной шкале: например, связь между полом и успешностью обучения) или от –1 до +1 (если обе переменные относятся, хотя бы к порядковой шкале: например, связь между уровнем образования и уровнем заработка). Полное отсутствие связи соответствует 0, максимальная связь наблюдается как при –1, так и при +1. Максимальная сила связи является научной идеализацией. Соответственно, в реальной жизни значения соответствующих коэффициентов принимают промежуточные значения между –1 и 0 или 0 и +1. Например, сила связи между ростом и весом мужчин равна +0,38, для женщин этот показатель равен всего лишь +0,18 (Украина, 2008 год).
Знак связи говорит о ее направлении. Отрицательная связь указывает, что при увеличении значений одной переменной, значения другой будут уменьшаться. Если же связь положительная, то значения обоих переменных будут изменяться в одном направлении. Связь между ростом и весом, как вы понимаете, является положительной. Следовательно, более высокие люди с большей вероятностью будут иметь и больший вес. Отрицательной, например, будет связь между количеством выпитого за ночь алкоголя и самочувствием с утра.
Более подробно анализ связей рассмотрен в следующей главе.
- default_titleХили Дж. Статистика. Социологические и маркетинговые исследования. - К.: ООО "ДиаСофтЮП"; СПб.: Питер, 2005. - 638 с.
- Show More