Интервальное оценивание
Во многих случаях бывает необходимо на основе единичного параментра выборки (среднее значение или пропорция) оценить соответствующий параметр генеральной совокупности. Если выборка достаточна большая (100 и более наблюдений), используя свойства кривой нормального распределения, а также центральную придельную теорему, можно построить интервал, в который с заданной вероятностью попадет истинное значение.
Как вы помните из второй главы, распределение выборочных средних имеет нормальный вид. Соответственно вероятность получения выборки со средним близким к среднему значению генеральной совокупности весьма высока. Но даже в тех случаях, когда среднее для выборки будет достаточно сильно отличаться от среднего генеральной совокупности, доверительный интервал [в подавляющем большинстве случаев] будет включать истинное значение. И лишь в очень редких случаях будут получены выборки с настолько сильно отличающимися параметрами выборки и генеральной совокупности, что истинное значение не попадет в доверительный интервал.
Мы не станем детальнее углубляться в соответствующие доказательства и примеры, а просто рассмотрим технику построения доверительных интервалов.
Доверительные интервалы для средних значений

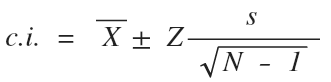
где Z - стандартизированное значение, определяемое уровнем альфа или p-значением (вероятностью того, что истинное значение не попадет в доверительный интервал);
s - стандартное отклонение по выборке;
n - размер выборки.
Очевидно что s и n известны нам из самого исследования. В свою очередь, Z определяется с помощью таблицы стандартизированных значений:

Доверительный уровень говорит о том, с какой вероятностью истинное значение попадет в построенный интервал.
Рассмотрим пример. Допустим из выборки (n = 300) известно, что среднее значение для месячного заработка киевлян составляет 4000 грн., а стандартное отклонение - 75 грн. Если нас удовлетворит вероятность ошибки равная 5% (альфа - 0,05), то Z = ±1,96.

Отсюда:

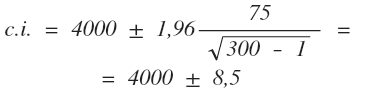
Таким образом, истинное значение для киевлян с вероятностью 95% должно попасть в интервал от 3991,5 грн. до 4008,5 грн.
Доверительные интервалы для пропорций

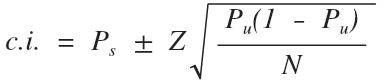
По сравнению с предыдущей, в данной формуле остался размер выборки и Z-значение. Последнее определяется оно также с помощью приведенной выше таблицы.
Другие составляющие следующие:
Ps - значение пропорции для выборки;
Pu - значение пропорции для генеральной совокупности.
У наиболее внимательных из вас мог возникнуть вопрос: откуда мы возьмем Pu, если мы хотим использовать Ps для его оценки? Или: если нам известно Pu, то зачем нам Ps? Действительно, Ps нам только и нужно для того, чтобы оценить неизвестное Pu. Выход из этой ситуации достаточно простой - за Pu принимают такую величину (как вы помните для пропорций оно может варьироваться от 0 до 1), которая бы дала нам наибольшее значение выражения Pu(1-Pu). В таком случае и сам доверительный интервал примет наибольшее значение (при прочих равных условиях). Фактически исследователь должен пойти на заведомое увеличение интервала, ведь больший интервал с большей вероятностью будет включать искомую истинную величину для генеральной совокупности. Таким значением является 0,5:
0,5(1-0,5) = 0,5*0,5 = 0,25
Теперь рассмотрим пример. Пусть, согласно результатам предвыборного опроса, за оппозиционную партию готово проголосовать 17% населения (Ps = 0,17), размер выборки составляет 1200 человек, а уровень альфа - 0,01. Тогда:

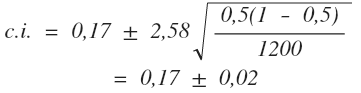
Следовательно с вероятностью в 99% за оппозиционную партию проголосует от 15% до 19% населения.