Модификация социологических данных средствами R
19/07/15 20:20 Относится к категории: Эмпирическая социология | Анализ данных | R | Социологическое образование

В случае использования числовой переменной с большим диапазоном возможных значений, следует проверить ее на наличие «выбросов» - нетипично больших или малых значений. Для визуализации последних можно использовать функцию boxplot(), позволяющую построить диаграмму размахов. В качестве данных создадим вектор значений «salary» на основании переменной «l3», исключив из нее респондентов без доходов и использовав только тех респондентов, которые были опрошены в рамках последнего этапа исследования, то есть в 2014 году.
finalUSind$salary <- NA
indexes <- which(finalUSind$l3 > 0 & finalUSind$year == 2014)
finalUSind$salary[indexes] <- finalUSind$l3[indexes]
boxplot(salary, horizontal = T, las = 1, col = "slategray3",
outpch = 16, outcol = "slategray3")
Полученная диаграмма (см. рис.1) показывает нижнюю и верхнюю границы «выбросов», квартили, медиану и сами «выбросы» (они отмечены точками).
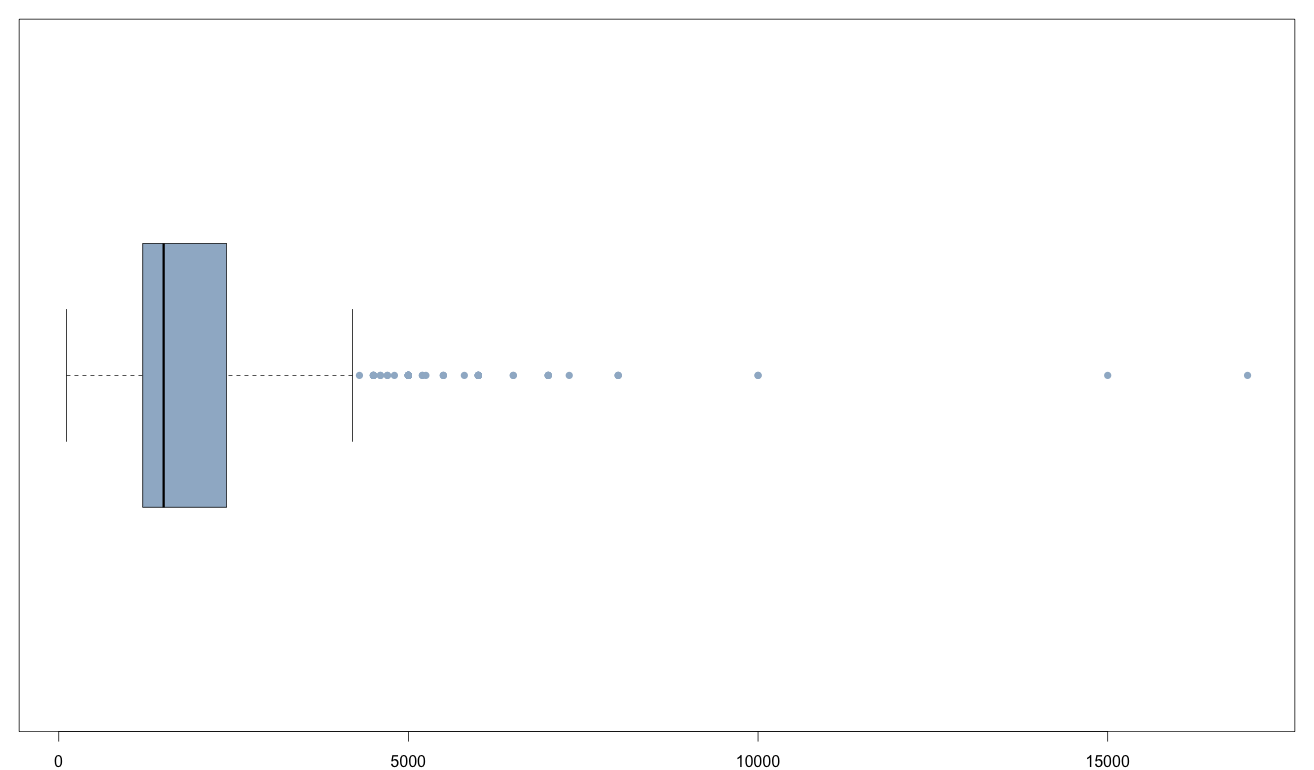
Рис. 1. Диаграмма размахов, построенная с помощью функции boxplot()
Для содержательной детализации числовых параметров этой диаграммы могут быть использованы функции boxplot.stats() и barplot(). Первая показывает нижнюю границу «выбросов» (вместо нее может быть показано минимальное значение, если оно больше нижней границы), первый квартиль, медиану, второй квартиль, верхнюю границу «выбросов» (может быть показано максимальное значение, если оно меньше верхней границы) [нижняя граница равна Q1 - 1,5 * IQR, а нижняя - Q3 + 1,5 * IQR, где Q1 - первый квартиль, Q3 - третий квартиль, IQR - межквартильная широта]. Вторая позволяет проанализировать частотное распределение «выбросов» с помощью столбчастой диаграммы (см.рис.2).
Для содержательной детализации числовых параметров этой диаграммы могут быть использованы функции boxplot.stats() и barplot(). Первая показывает нижнюю границу «выбросов» (вместо нее может быть показано минимальное значение, если оно больше нижней границы), первый квартиль, медиану, второй квартиль, верхнюю границу «выбросов» (может быть показано максимальное значение, если оно меньше верхней границы) [нижняя граница равна Q1 - 1,5 * IQR, а нижняя - Q3 + 1,5 * IQR, где Q1 - первый квартиль, Q3 - третий квартиль, IQR - межквартильная широта]. Вторая позволяет проанализировать частотное распределение «выбросов» с помощью столбчастой диаграммы (см.рис.2).
boxplot.stats(salary)$stats
[1] 110 1200 1500 2400 4200
barplot(table(boxplot.stats(salary)$out),horiz = T,
las = 1, col = "slategray3")
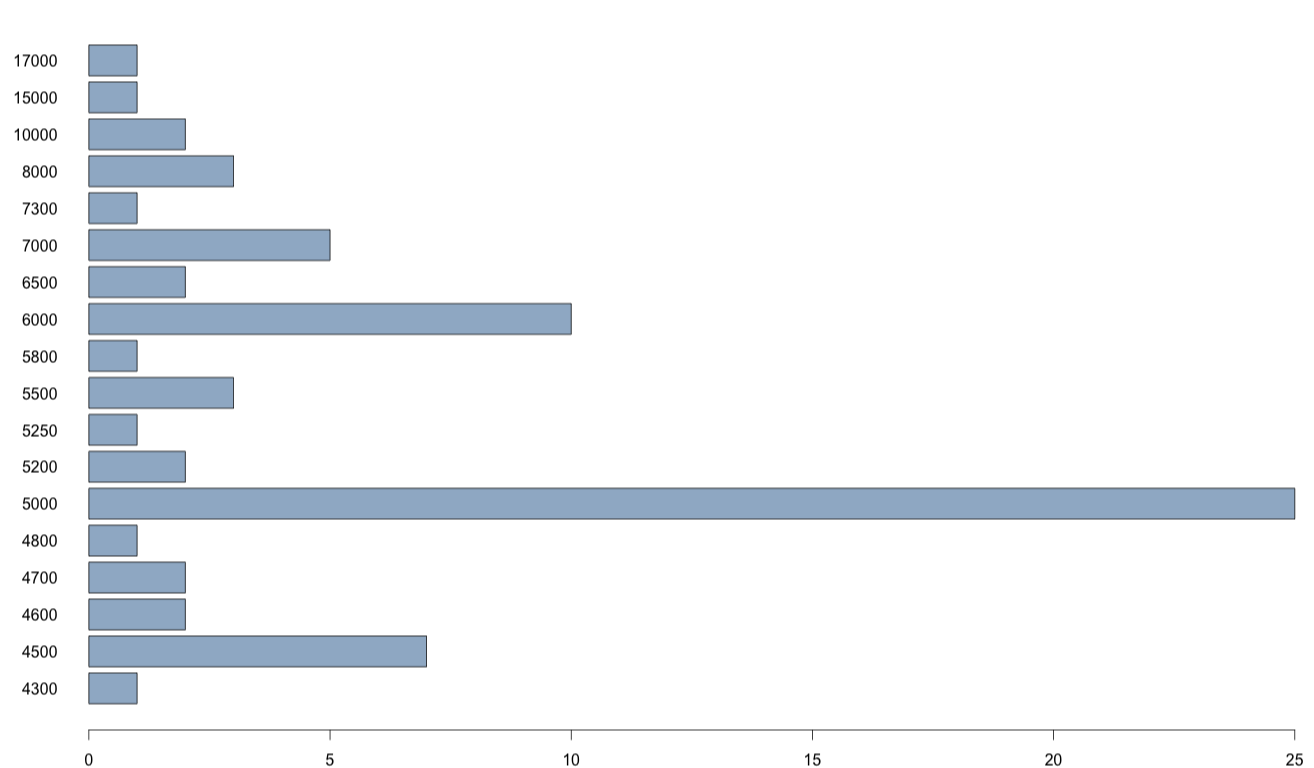
Рис. 2. Столбчастая диаграмма, построенная с помощью функции barplot()
Решение о том, что же в итоге следует считать выбросом, всегда является несколько субъективным и основывается на интерпретации полученных результатов. В этом примере мы решили, что выбросами будут все значения равные или превышающие 10000. Для того, чтобы создать новую переменную, не содержащую выбросов, можно использовать следующую команду:
finalUSind$l3new <- finalUSind$l3[finalUSind$l3 < 10000]
Порой возникает необходимость преобразования той или иной переменной исходя из требований, предъявляемых к анализируемым данным со стороны используемого метода. Также может потребоваться приведение различных шкал к одной размерности. Примерами таких ситуаций являются, соответственно, использование кластерного анализа и построение линейных графиков. Так, в рамках кластерного анализа переменные с более широким диапазоном значений будут иметь большее влияние на образование кластеров, что далеко не всегда оправдано. Что же до построения линейных графиков, то анализ переменных с более узким диапазоном значений будет затруднен. В таких случаях подойдет нормализация или расчет Z-значений:
Решение о том, что же в итоге следует считать выбросом, всегда является несколько субъективным и основывается на интерпретации полученных результатов. В этом примере мы решили, что выбросами будут все значения равные или превышающие 10000. Для того, чтобы создать новую переменную, не содержащую выбросов, можно использовать следующую команду:
finalUSind$l3new <- finalUSind$l3[finalUSind$l3 < 10000]
Порой возникает необходимость преобразования той или иной переменной исходя из требований, предъявляемых к анализируемым данным со стороны используемого метода. Также может потребоваться приведение различных шкал к одной размерности. Примерами таких ситуаций являются, соответственно, использование кластерного анализа и построение линейных графиков. Так, в рамках кластерного анализа переменные с более широким диапазоном значений будут иметь большее влияние на образование кластеров, что далеко не всегда оправдано. Что же до построения линейных графиков, то анализ переменных с более узким диапазоном значений будет затруднен. В таких случаях подойдет нормализация или расчет Z-значений:
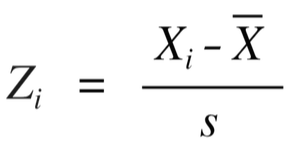
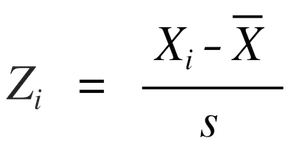
Допустим, мы хотим разделить респондентов на группы в зависимости от их роста и веса. Для нормализации в R используется функция scale():
data$rost <- scale(finalUSind$g7)
data$ves <- scale(finalUSind$g8)
Переменная g7 включает информацию про рост респондента (интерквартельная широта равна 96 см.), а g8 - про вес (интерквартельная широта равна 17 кг.). После стандартизации влияние размерности шкалы на результаты кластерного анализа будет нивелировано (в данном случае мы исходим их того, что обе переменные одинаково важны в процессе разделения респондентов на группы).
Теперь рассмотрим пример, касающийся изменения уровней интернальности/экстернальности (интерналы объясняют изменения в своей жизни внешними и не зависящими от них обстоятельствами, экстерналы - наоборот берут ответственность на себя) и материальной обеспеченности респондентов в целом по стране. Для анализа использованы линейные графики. Но прежде, чем их построить, необходимо рассчитать соответствующие индексы. В случае оценки материального положения семьи (используется шкала от 0 до 10, где 0 - самая низкая оценка, 10 - самая высокая) достаточно рассчитать среднее значение для каждого года. Для этого можно использовать функцию aggregate():
data$rost <- scale(finalUSind$g7)
data$ves <- scale(finalUSind$g8)
Переменная g7 включает информацию про рост респондента (интерквартельная широта равна 96 см.), а g8 - про вес (интерквартельная широта равна 17 кг.). После стандартизации влияние размерности шкалы на результаты кластерного анализа будет нивелировано (в данном случае мы исходим их того, что обе переменные одинаково важны в процессе разделения респондентов на группы).
Теперь рассмотрим пример, касающийся изменения уровней интернальности/экстернальности (интерналы объясняют изменения в своей жизни внешними и не зависящими от них обстоятельствами, экстерналы - наоборот берут ответственность на себя) и материальной обеспеченности респондентов в целом по стране. Для анализа использованы линейные графики. Но прежде, чем их построить, необходимо рассчитать соответствующие индексы. В случае оценки материального положения семьи (используется шкала от 0 до 10, где 0 - самая низкая оценка, 10 - самая высокая) достаточно рассчитать среднее значение для каждого года. Для этого можно использовать функцию aggregate():
finalUSind$l2num <- as.numeric(finalUSind$l2)
indfirst <- aggregate(finalUSind$l2num,
by=list(finalUSind$year),
FUN=mean, na.rm = T)
indfirstfin <- scale(indfirst$x)
Что касается индекса экстернальности/интернальности, то расчет будет более сложным. Сначала создадим и запишем в объект lineGraph таблицу сопряженности (см.табл.) с помощью следующего синтаксиса (внешний вид таблицы отредактирован в соответствии с форматом статьи):
lineGraph <- table(finalUSind$year,finalUSind$f4)
lineGraph <- table(finalUSind$year,finalUSind$f4)
| Год | Варианты ответа | ||||
| В основном от внешних обстоятельств | В некоторой мере от меня, но больше от внешних обстоятельств | В одинаковой мере от меня и от внешних обстоятельств | В большей мере от меня, чем от внешних обстоятельств | В основном от меня | |
| 1992 | 358 | 611 | 450 | 215 | 115 |
| 1994 | 509 | 553 | 385 | 180 | 166 |
| 1995 | 528 | 513 | 409 | 186 | 166 |
| ... | ... | ... | ... | ... | ... |
| 2010 | 289 | 550 | 560 | 211 | 189 |
| 2012 | 303 | 581 | 549 | 184 | 183 |
| 2014 | 296 | 508 | 548 | 255 | 191 |
Теперь для каждого года необходимо из суммы наблюдений, попадающих в первые две категории, отняться сумму для двух последних, а полученное значение разделить на общее количество наблюдений, после чего можно стандартизировать индекс:
indsec <- (rowSums(lineGraph[4:5,]) - rowSums(lineGraph[1:2,]) / rowSums(lineGraph) indsecfin <- scale(indsec)
Далее приведены два графика (см.рис.3): первый построен на основании «сырых» индексов, второй - нормализированных. В первом случае связь переменных практически невозможно проследить, во втором - она выражена очень отчетливо.
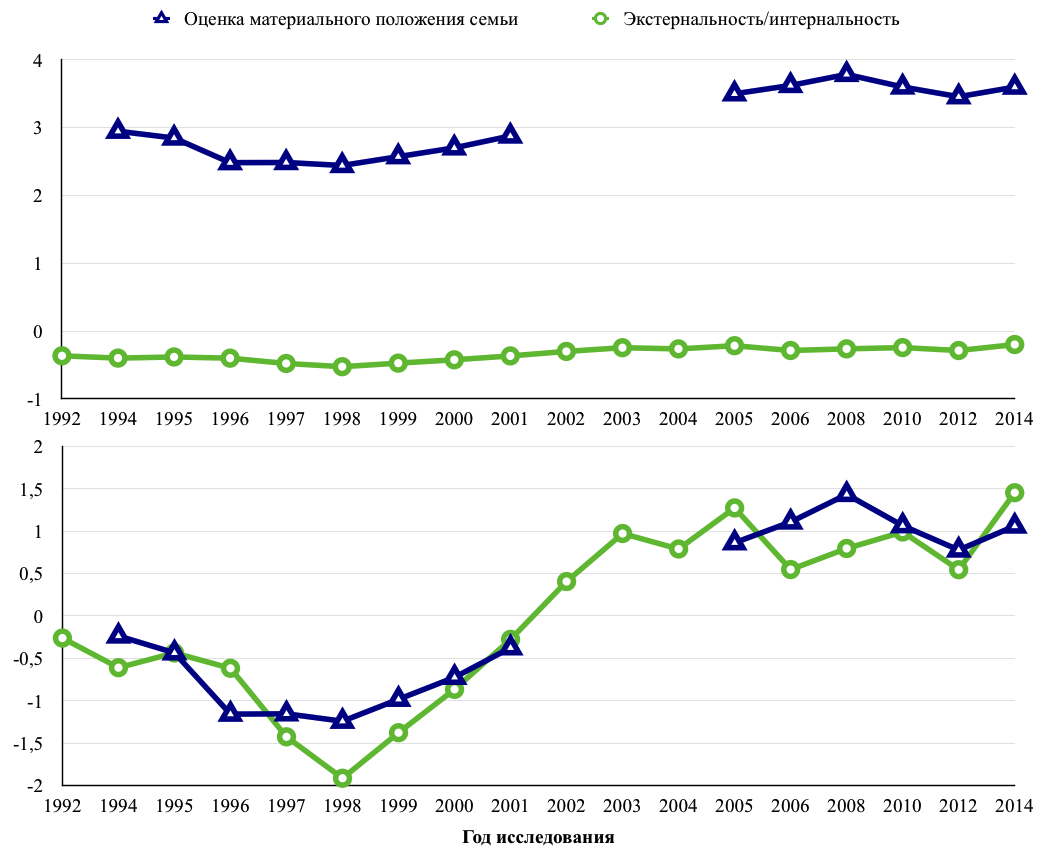
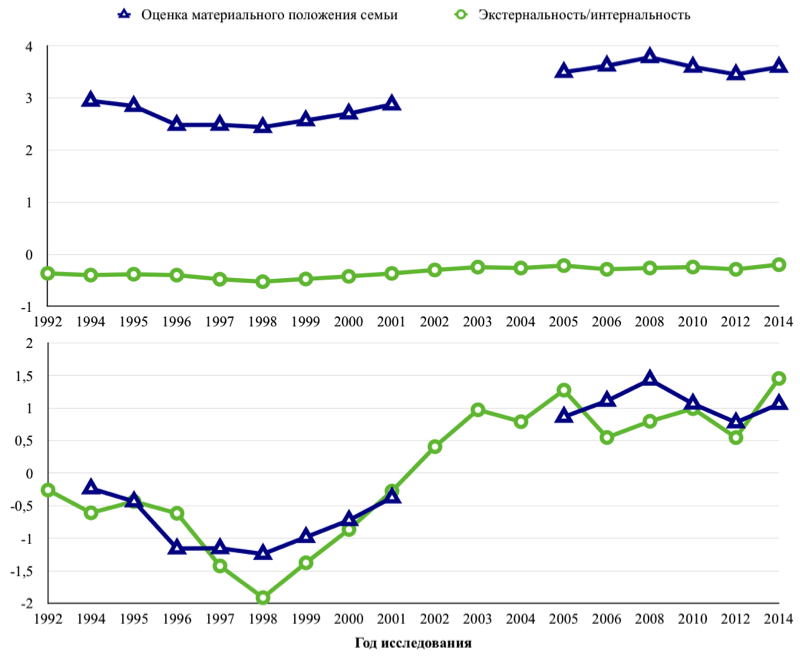
Рис. 3. Линейный график до (а) и после (б) нормализации значений
Другими распространенными способами преобразования являются логарифмическое, квадратного корня, обратное и квадратное [Шипунов в соавт., 2014: с. 62-64]. Логарифмическое преобразование может дать нормальное распределение, когда оно скошено вправо. Кроме того, оно делает зависимости между переменными более линейными и уравнивает дисперсии. Поскольку логарифмическое преобразование непригодно для работы с нулями, рекомендуется прибавлять единицу:
log(data$var1 + 1)
Преобразование квадратного корня похоже по действию на логарифмическое. При этом оно может работать с нулями, но не может - с отрицательными значениями:
sqrt(data$var1)
Обратное преобразование используется в случае необходимости стабилизации дисперсии. Также как и логарифмическое предполагает добавление единицы:
1/(data$var1 +1)
Квадратное преобразование подходит для случаев, когда распределение скошено влево (может привести к нормальному). Оно линеаризует зависимости и выравнивает дисперсии:
data$var1^2
Кроме описанных способов модификации, часто возникает необходимость расчета новых переменных (как на основании условий специальных методик, которые применялись в рамках исследования, так и отталкиваясь от своего опыта на основании отдельных переменных), а также перекодировки имеющихся (например, распределение респондентов по возрастным категориями или регионам проживания).
При необходимости дихотомизации числовой переменной можно использовать функцию ifelse(). В качестве входящих данных опять использованы ответы респондентов в 2014 году про доход за последний месяц. При этом не исключены те, у кого доход отсутствует:
num.data <- finalUSind$l3[finalUSind$year == 2014]
poor.and.rich <- ifelse(num.data <= 1500, 0, 1)
Функция ifelse() принимает три аргумента: 1) логическое условие (в нашем случае - доход больше 1500); 2) значение, возвращаемое функцией в случае истинности условия для респондента (в нашем случае - ноль); 3) значение возвращаемое в случае ложности условия для респондента (в нашем случае - 1).
Вторым простым способом разбивки числовых переменных является автоматизированная процедура категоризации с помощью функции bin.var(), позволяющая применить один из трех методов: 1) построение интервалов равных размеров (величина интервала равна Xmax/n, где Xmax - максимальное значение в распределении, n - количество интервалов); 2) построение интервалов одинаковой наполненности (по N/n респондентов в каждой группе, где N - размер выборки, n - количество интервалов); 3) построение интервалов на основании кластеризации методом k-средних. Сначала рассмотрим общую форму соответствующей команды:
Другими распространенными способами преобразования являются логарифмическое, квадратного корня, обратное и квадратное [Шипунов в соавт., 2014: с. 62-64]. Логарифмическое преобразование может дать нормальное распределение, когда оно скошено вправо. Кроме того, оно делает зависимости между переменными более линейными и уравнивает дисперсии. Поскольку логарифмическое преобразование непригодно для работы с нулями, рекомендуется прибавлять единицу:
log(data$var1 + 1)
Преобразование квадратного корня похоже по действию на логарифмическое. При этом оно может работать с нулями, но не может - с отрицательными значениями:
sqrt(data$var1)
Обратное преобразование используется в случае необходимости стабилизации дисперсии. Также как и логарифмическое предполагает добавление единицы:
1/(data$var1 +1)
Квадратное преобразование подходит для случаев, когда распределение скошено влево (может привести к нормальному). Оно линеаризует зависимости и выравнивает дисперсии:
data$var1^2
Кроме описанных способов модификации, часто возникает необходимость расчета новых переменных (как на основании условий специальных методик, которые применялись в рамках исследования, так и отталкиваясь от своего опыта на основании отдельных переменных), а также перекодировки имеющихся (например, распределение респондентов по возрастным категориями или регионам проживания).
При необходимости дихотомизации числовой переменной можно использовать функцию ifelse(). В качестве входящих данных опять использованы ответы респондентов в 2014 году про доход за последний месяц. При этом не исключены те, у кого доход отсутствует:
num.data <- finalUSind$l3[finalUSind$year == 2014]
poor.and.rich <- ifelse(num.data <= 1500, 0, 1)
Функция ifelse() принимает три аргумента: 1) логическое условие (в нашем случае - доход больше 1500); 2) значение, возвращаемое функцией в случае истинности условия для респондента (в нашем случае - ноль); 3) значение возвращаемое в случае ложности условия для респондента (в нашем случае - 1).
Вторым простым способом разбивки числовых переменных является автоматизированная процедура категоризации с помощью функции bin.var(), позволяющая применить один из трех методов: 1) построение интервалов равных размеров (величина интервала равна Xmax/n, где Xmax - максимальное значение в распределении, n - количество интервалов); 2) построение интервалов одинаковой наполненности (по N/n респондентов в каждой группе, где N - размер выборки, n - количество интервалов); 3) построение интервалов на основании кластеризации методом k-средних. Сначала рассмотрим общую форму соответствующей команды:
bin.var(salary[salary < 10000], bins=4,
method="intervals", labels=NULL))
В качестве первого аргумента указывается числовая переменная массива или вектор (как в нашем случае), в качестве второго (bins) - количество интервалов, которые необходимо построить, в качестве третьего (method) - метод разбивки, с помощью последнего (labels) задается формат наименования групп. Теперь проанализируем к каким результатам приводит каждый из трех методов (для наглядности, результаты приводятся в отредактированном виде):
table(bin.var(salary[salary < 10000], bins=4,
method="intervals", labels=NULL))
(102,2080] 1115
(2080,4060] 383
(4060,6030] 56
(6030,8010] 11
table(bin.var(salary[salary< 10000], bins=4,
method="proportions", labels=NULL))
(110,1190] 392
(1190,1500] 397
(1500,2400] 388
(2400,8000] 388
table(bin.var(salary[salary< 10000], bins=4,
method="natural", labels=NULL))
(-Inf,1450] 678
(1450,2400] 499
(2400,4200] 322
(4200,8000] 66
Как видно, в случае анализа доходов наиболее сбалансированную структуру (как в смысле величины интервалов, так и в смысле наполненности категорий) обеспечивает использование третьего метода.
В случае перекодировки номинальных переменных, а также в случае необходимости полного контроля при создании нескольких категорий на основании числовой переменной, наилучшим способом является использование функции within(). Для примера рассмотрим перекодировку переменной о семейном статусе респондента с шестью категориями: 1 - «Никогда не был(-а) в браке», 2 - «Состою в зарегестированном браке», 3 - «Состою в фактическом, незарегистрированном браке», 4 - «Разведен(-а) официально», 5 - «Разошелся(-ась), хотя официально не розведен(-а)», 6 - «Вдовец (вдова)». Новая переменная будет иметь четыре категории: «Никогда не был(-а) в браке» (первая категория), «Состою в браке (гражданском или фактическом)» (вторая и третья категории), «Разошелся или разведен» (четвертая и пятая категории), «Вдовец (вдова)» (шестая категория). Синтаксис R следующий:
В случае перекодировки номинальных переменных, а также в случае необходимости полного контроля при создании нескольких категорий на основании числовой переменной, наилучшим способом является использование функции within(). Для примера рассмотрим перекодировку переменной о семейном статусе респондента с шестью категориями: 1 - «Никогда не был(-а) в браке», 2 - «Состою в зарегестированном браке», 3 - «Состою в фактическом, незарегистрированном браке», 4 - «Разведен(-а) официально», 5 - «Разошелся(-ась), хотя официально не розведен(-а)», 6 - «Вдовец (вдова)». Новая переменная будет иметь четыре категории: «Никогда не был(-а) в браке» (первая категория), «Состою в браке (гражданском или фактическом)» (вторая и третья категории), «Разошелся или разведен» (четвертая и пятая категории), «Вдовец (вдова)» (шестая категория). Синтаксис R следующий:
finalUSind <- within(finalUSind,{
s3_4 <- NA
s3_4[as.numeric(s3) == 1] <- 1
s3_4[as.numeric(s3) == 2] <- 2
s3_4[as.numeric(s3) == 3] <- 2
s3_4[as.numeric(s3) == 4] <- 3
s3_4[as.numeric(s3) == 5] <- 3
s3_4[as.numeric(s3) == 6] <- 4
})
В первой строке мы указываем название массива, в котором осуществляются преобразования (finalUSind), во второй присваиваем новой переменной пропуски (этот шаг обязательный), в дальнейших с помощью логических выражений определяем условия для сопоставление старых и новых категорий. Используя другие логические операторы и «перевернув» порядок присвоения значений можно сократить приведенный синтаксис:
finalUSind <- within(finalUSind,{
s3_4 <- NA
s3_4[as.numeric(s3) == 6] <- 4
s3_4[as.numeric(s3) < 6] <- 3
s3_4[as.numeric(s3) < 4] <- 2
s3_4[as.numeric(s3) == 1] <- 1
})
Еще одним альтернативным вариантом в данном случае будет такой (здесь порядок присвоения не играет роли):
finalUSind <- within(finalUSind,{
s3_4 <- NA
s3_4[as.numeric(s3) == 6] <- 4
s3_4[as.numeric(s3) == 2 | as.numeric(s3) == 3] <- 2
s3_4[as.numeric(s3) == 4 | as.numeric(s3) == 5] <- 3
s3_4[as.numeric(s3) == 1] <- 1
})
Когда необходимо вычислить новую переменную на основании имеющихся, используются привычные математические операции: + (сложение), - (вычитание), * (умножение), / (деление), ^ или ** (возведение в степень). Также могут использоваться и встроенные в R функции. Для начала рассмотрим построение индекса пропорциональности веса. Он рассчитывается как отношение веса тела человека в килограммах к квадрату его роста в метрах. Исходя из того, что в массиве рост зафиксирован в сантиметрах, а вес - в килограммах, синтаксис может принять один из двух вариантов:
finalUSind$g8and7 <- finalUSind$g8/(finalUSind$g7*finalUSind$g7/10000)
finalUSind$g8and7 <- finalUSind$g8/(finalUSind$g7**2/10000)
В случае, когда необходимо вычислить большее количество новых переменных, удобно использовать функцию transform(). Например, при переводе переменных, содержащих информацию в гривнях (доход респондента, минимально приемлемый уровень дохода по его оценке, уровень дохода при котором по мнению респондента можно жить хорошо и т.д.), использование этой функции будет выглядеть следующим образом:
finalUSind$g8and7 <- finalUSind$g8/(finalUSind$g7*finalUSind$g7/10000)
finalUSind$g8and7 <- finalUSind$g8/(finalUSind$g7**2/10000)
В случае, когда необходимо вычислить большее количество новых переменных, удобно использовать функцию transform(). Например, при переводе переменных, содержащих информацию в гривнях (доход респондента, минимально приемлемый уровень дохода по его оценке, уровень дохода при котором по мнению респондента можно жить хорошо и т.д.), использование этой функции будет выглядеть следующим образом:
finalUSind <- transform(finalUSind,
l3_dollar = l3 / currency,
l5_dollar = l5 / currency,
l6_dollar = l6 / currency,
l7_dollar = l7 / currency,
l8_dollar = l8 / currency,
l9_dollar = l9 / currency,
l10_dollar = l10 / currency,
l11_dollar = l11 / currency,
l12_dollar = l12 / currency,
)
В первой строке указан массив (до знака присваивания), в который записываются новые переменные, и из которого берутся переменные для расчета (в качестве первого аргумента функции). Далее приведены выражения для расчета всех необходимы переменных (переменная «currency» несет в себе информацию про курс доллара).
Во многих случаях при расчете новых переменных очень удобно использовать встроенные, то есть доступные в R по умолчанию, функции. Хорошим примером является расчет Интегрального индекса социального самочувствия, разработанного Евгением Головахой и Наталией Паниной [Головаха, Панина, 1997]. На первом этапе расчета этого индекса необходимо найти сумму значений по 20-ти индикаторам. Сначала рассмотрим синтаксис без использования встроенной функции:
Во многих случаях при расчете новых переменных очень удобно использовать встроенные, то есть доступные в R по умолчанию, функции. Хорошим примером является расчет Интегрального индекса социального самочувствия, разработанного Евгением Головахой и Наталией Паниной [Головаха, Панина, 1997]. На первом этапе расчета этого индекса необходимо найти сумму значений по 20-ти индикаторам. Сначала рассмотрим синтаксис без использования встроенной функции:
finalUSindTest <- transform(finalUSindTest,
f6_sum = as.numeric(f6_1) +
as.numeric(f6_2) + as.numeric(f6_3)
+ as.numeric(f6_4) + as.numeric(f6_5)
+ as.numeric(f6_6) + as.numeric(f6_7)
+ as.numeric(f6_8) + as.numeric(f6_9)
+ as.numeric(f6_10) + as.numeric(f6_11)
+ as.numeric(f6_12) + as.numeric(f6_13)
+ as.numeric(f6_14) + as.numeric(f6_15)
+ as.numeric(f6_16) + as.numeric(f6_17)
+ as.numeric(f6_18) + as.numeric(f6_19)
+ as.numeric(f6_20))
В целях компактности здесь можно использовать функцию rowSums(), но перед этим все индикаторы необходимо привести к числовому виду (функция принимает только числовые переменные, а сейчас они являются переменными-факторами). Для этого использован цикл for():
for (i in 184:203) {
finalUSind[[as.character(i)]] <- as.numeric(finalUSind[[i]])
}
finalUSind$f6_sum <- rowSums(finalUSind[558:577])
Как в цикле, так и при использовании функции rowSums() обращение к переменным осуществляется не с помощью имен переменным, а с помощью их индексов. Переменным с f6_1 по f6_20 соответствуют индексы со 184-го по 203-й, а их оцифрованным копиям – с 558-го по 577-й. Как видно в данном случае для суммирования индикаторов понадобилось значительно меньше строк кода.
Далее необходимо скорректировать полученную переменную (f6_sum) с учетом того, что категория представленная четверкой («Не интересует») при расчете индекса должна быть принята за двойку. Следовательно, сумма двадцати индикаторов должна давать максимум 60, а не 80 баллов. Для решения этой задачи необходимо подсчитать для каждого респондента количество четверок и вычесть соответствующее значение умноженное на два из суммарного индекса. Здесь мы также используем цикл for():
Далее необходимо скорректировать полученную переменную (f6_sum) с учетом того, что категория представленная четверкой («Не интересует») при расчете индекса должна быть принята за двойку. Следовательно, сумма двадцати индикаторов должна давать максимум 60, а не 80 баллов. Для решения этой задачи необходимо подсчитать для каждого респондента количество четверок и вычесть соответствующее значение умноженное на два из суммарного индекса. Здесь мы также используем цикл for():
finalUSind$f6_min <- 0
for (i in 184:203) {
min <- finalUSind[i] == 4
finalUSind$f6_min <- finalUSind$f6_min + min
}
finalUSind$f6_sum <- finalUSind$f6_sum - finalUSind$f6_min*2
finalUSind$f6_min <- NULL
Первая команда в теле цикла создает набор значений, состоящих из TRUE (истина), если значение переменной равно четырем, и FALSE (ложь), если - нет. Поскольку истина в математических операциях принимается за единицу, а ложь - за ноль, легко посчитать количество четверок по каждому респонденту (для этого используется переменная f6_min). Последняя строка синтаксиса удаляет счетчик четверок, поскольку для дальнейшей работы он не нужен.
Литература:
1) Головаха Е. Интегральный индекс социального самочувствия (ИИСС): конструирование и применение социологического теста в массовых опросах / Евгений Головаха, Наталия Панина. – К.: Институт социологии НАН Украины, 1997. – 64 с.
2) Шипунов А. Наглядная статистика. Используем R! / Алексей Шипунов, Евгений Балдин, Полина Волкова, Антон Коробейников, София Назарова, Сергей Петров, Вадим Суфиянов. - М.: ДМК Пресс, 2012, - 298 с.
Литература:
1) Головаха Е. Интегральный индекс социального самочувствия (ИИСС): конструирование и применение социологического теста в массовых опросах / Евгений Головаха, Наталия Панина. – К.: Институт социологии НАН Украины, 1997. – 64 с.
2) Шипунов А. Наглядная статистика. Используем R! / Алексей Шипунов, Евгений Балдин, Полина Волкова, Антон Коробейников, София Назарова, Сергей Петров, Вадим Суфиянов. - М.: ДМК Пресс, 2012, - 298 с.
blog comments powered by Disqus