Основы программирования: авторские функции

03/01/14 19:22 Относится к категории: Анализ данных | R

Во многих случаях (когда необходимо решить специфическую задачу) можно обойтись написанием скрипта (здесь имеется ввиду программный код для конкретного случая) по типу того, который приведен в предыдущей статье (создание фреймов данных для каждого года и запись их в список). Маловероятно, что такие скрипты понадобятся в дальнешем. Поэтому их специфическая адаптация для других ситуаций не требуется.
Вместе с тем, возникают и ситуации, когда необходимо написать такой программный код, который бы решал одну и ту же задачу, возникающую часто и требующую учета изменяющихся ключевых данных. По этой причине, в процессе работы можно применять не только уже имеющиеся функции, но и создавать свои собственные. Такие авторские функции позволяют использовать уже имеющиеся в R функции, условные операторы, циклы, списки и многое другое. Для многих языков программирование функциональное программирование является одной из основ. В случае R (если мы говорим про анализ данных) многие задачи уже реализованы как в базовой версии, так и виде расширений. Несмотря на это, функциональное программирование в R также является важным дополнением, существенно расширяющим возможности исследователя.

Создание авторской функции
Для создания авторской функции используется функция function(), состоящая из двух компонентов: а) тех аргументов, которые принимает функция (входящие данные; в некоторых случаях они могут и не понадобиться); б) синтаксис, который при использовании входящих данных решает задачи исследователя; если синтаксис включает единственное выражение, то вводится в той же строке, где объявляется функция, в других случаях он размещается в фигурных скобках.
Рассмотрим элементарные примеры (исключительно в дидактических целях):

  > fun1 <- function(x1, x2) print(x1+x2)
  > fun1(1, 2)
  [1] 3
  > fun2 <- function(x1, x2) {
      x3 <- x1+x2
      print(x3/x2)
    }
  > fun2(1, 2)
  [1] 1.5

Первая функция (fun1()) необходима для того, чтобы найти сумму двух значений. Сначала мы указываем, что функция примет два значения - x1 и x2, после чего прописываем действие с ними - вывод на экран их суммы с помощью функции print(). Во второй строке синтаксиса мы используем функцию. Для этого необходимо ввести ее имя и указать в скобках те значения, которыми являются x1 и x2. Поскольку x1 мы принимаем за "1", а х2 - за "2", итогом будет "3".
Следующая функция включает более одного выражения, поэтому ее синтаксис прописан в фигурных скобках. Как и в предыдущем случае она принимает два значения - x1 и x2. Далее эти значения складываются и записываются в x3, после чего с помощью функции print() на экран выводится результат от деления х3 на х2. Использовав те же аргументы, что и в первой функции, мы получим "1,5".
Одной из особенностей авторских функций является то, что все объекты, которыми оперирует функция являются внутренними, то есть они недоступны за пределами функции. Поэтому в случаях, когда необходимо получить определенный результат "на выходе", используется функция return(). Для того, чтобы понять как она работает, изменим вторую авторскую функцию (fun2()):

  > fun2 <- function(x1, x2) {
      x3 <- x1+x2
      return(x3/x2)
    }
  > result <- fun2(1, 2)
  > result
  [1] 1.5

Теперь функция вместо того, чтобы выводить x3/x2 с помощью print(), она возвращает это выражение с помощью return(). И это будет тот результат, который мы можем передать (записать) какому-либо объекту. В нашем случае мы записываем результат выполнения функции в объект result. После этого мы выводи его на экран. Авторская функция может возвращать самые разные объекты (скаляры, векторы, списки и так далее).

Теперь рассмотрим более содержательные примеры.
Авторская функция для расчета коэффициента изменчивости категорий (IQV)
Для чего нужен коэффициент изменчивости категорий, какова его формула и пример ее использования вы можете посмотреть здесь. Как видно, для расчета IQV необходимо знать количество категорий переменной, частоту каждой категории и количество наблюдений (которое, впрочем, является суммой частот). Следовательно, функция будет включать три аргумента (хотя можно обойтись и меньшим числом). Касательно синтаксиса функции: поскольку формула представлена в виде обыкновенной дроби, постольку синтаксис будет находить числитель, знаменатель и уже потом результат деления.
Итак:

  > IQV <- function(f_vector,k,N) {
      numerator <- k*(N^2 - sum(f_vector^2))
      denominator <- N^2*(k-1)
      iqv <- numerator/denominator
      return(iqv)
    }
  > freq <- c(30,20,10)
  > kat <- length(freq)
  > total <- sum(freq)
  > IQV(freq,kat,total)
  [1] 0.9166667

После создания функции, готовятся данные, соответствующие одномерному распределению и его параметрам, необходимым для вычисления IQV. Далее эти данные используются в качестве аргументов функции. Как видно, для реализации этой функции достаточно всего одного аргумента - f_vector, из которого могут быть выведены все остальные.

Авторская функция для расчета количества эффективных партий
В одном из своих недавних исследований меня интересовали три электоральных показателя по всем странам мира: а) количество всех партий, прошедших в парламент страны; б) количество релевантных партий в парламенте (более 3%); в) количество эффективных партий.
Последний показатель является в некотором смысле абстрактной величиной, которая рассчитывается по следующей формуле:

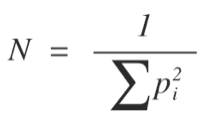
здесь "p" обозначает пропорцию мест в парламенте i-той партии.
Осуществлять расчет в ручную или с помощью Excel было неудобно. Поэтому я написал функцию, которая бы сообщала мне четыре показателя (кроме уже указанных - общее количество мест в парламенте). При этом пришлось использовать цикл, условный оператор, список и ряд уже имеющихся в R функций:

  > schitalka <- function(seats) {
      forEachParty <- list() # создаем пустой список, он понадобится
      relevant <- 0 # приравниваем количество релевантных партий к 0
      totalSeats <- sum(seats) # находим общее количество мест в парламенте
      for (i in 1:length(seats)) {
        p2 <- (seats[i] / totalSeats)^2 # для каждой партии находим "р" в квадрате
        forEachParty[[i]] <- p2 # записываем предыдущую величину в список
        if (seats[i] / sum(seats) > 0.03) relevant <- relevant+1 # если количество мест партии превышает 3% увеличиваем relevant на 1
      }
      numberOfEP <- 1 / sum(as.vector(forEachParty, mode="numeric")) # находим количество эффективных партий
      cat("к-во партий             :", length(seats), "\n") # здесь и далее выводим показатели на экран
      cat("к-во релевантных партий :", relevant, "\n")
      cat("к-во эффективных партий :", numberOfEP, "\n")
      cat("общее количество мест   :", totalSeats, "\n")
    }
  > schitalka(c(12,8,1)) # запускаем функцию, в качестве аргумента используется количество мест, полученных каждой партией в парламенте
  к-во партий             : 3 
  к-во релевантных партий : 3 
  к-во эффективных партий : 2.110048 
  общее количество мест   : 21

статью подготовил кандидат социологических наук Сергей Дембицкий

Вверх

Тэги: Анализ статистических данных, Среда статистических вычислений R, Аналіз статистичних даних, Середовище статистичних розрахунків R