Алгоритм сравнения социально-демографических групп: на примере установок на гражданскую активность

Создаем переменную-фактор, которая включает информацию о поле (мужчины, женщины), возрастной группе (молодежь, средний возраст, пожилой возраст) и регионе проживания (запад, центр, юго-восток) респондента. Всего 18 групп.

US2016$demog <- paste(US2016$r3, US2016$vg, sep = ".")
US2016$demog <- paste(US2016$demog, US2016$V278, sep = ".")
US2016$demog <- paste(US2016$demog, ".", sep = "")
US2016$demog <- as.factor(US2016$demog)
table(US2016$demog)

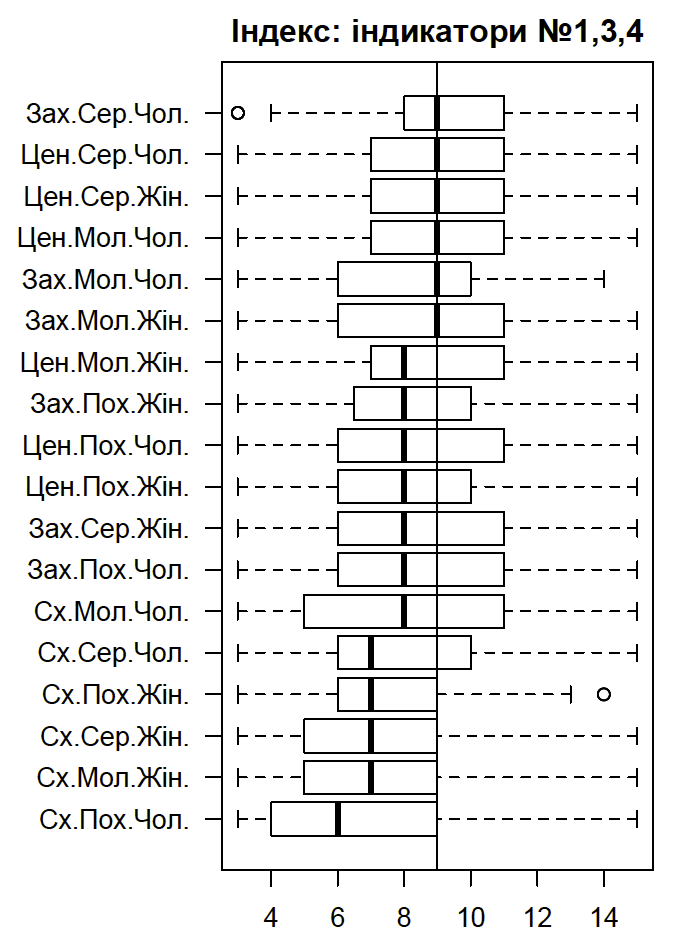
Упорядочиваем эту переменную в соответствии с медианами и первыми квартилями социально-демографических групп (для лучшего представления с помощью диаграммы размахов, см. рис. выше).

oind <- order(as.numeric(by(US2016$gp1, US2016$demog, median, na.rm = T)),
              as.numeric(by(US2016$gp1, US2016$demog, 
                            function(x)quantile(x, na.rm = T)[2])))    
US2016$demog1 <- ordered(US2016$demog, levels=levels(US2016$demog)[oind])
levels(US2016$demog1)

Осуществляем попарные сравнения всех групп (153 сравнения) с мопощью теста Вилкоксона и записываем их в вектор testM. Важно, чтобы вектор был наименованный. Иначе в дальнейшем будет очень сложно понять, какие пары показали статистически значимые различия. Это реализовано с помощью функции paste().

testM <- c()
x <- 1
while(x < 19) {
    for(i in x:18) {
        if(i != x) {
            testM[paste(levels(US2016$demog1)[i], levels(US2016$demog1)[x], sep = " VS ")] <- 
                wilcox.test(US2016$gp1[US2016$demog1 == levels(US2016$demog1)[i]],
                            US2016$gp1[US2016$demog1 == levels(US2016$demog1)[[x]]])$p.value
        }
    }
    x <- x+1
}

Осуществляем контроль множественных проверок с помощью метода Беньямини-Хохберта. При этом устанавливаем допустимую долю ложно отклоненных гипотез на уровне 5%. Записываем в вектор testF результаты, для которых принята альтернативная гипотеза.

testF <- p.adjust(testM, method = "BH")
testF <- testF[testF < 0.05]

Создаем матрицу forPlot 18 на 18, состоящую из 0. Наименуем строки и столбцы согласно 18 соц-дем группам, которые сравнивались. Создаем список labForMatr, элементы которого содержат информацию о группах, для которых была принята альтернативная гипотеза. Используем этот список для внесения в матрицу единиц для тех пар, по которым была принята альтернативная гипотеза.

forPlot <- matrix(0, ncol = 18, nrow = 18)
rownames(forPlot) <- levels(US2016$demog1)
colnames(forPlot) <- levels(US2016$demog1)

labForMatr <- strsplit(labels(testF), " VS ")

for (i in 1:length(labForMatr)) {
    forPlot[labForMatr[[i]][1],labForMatr[[i]][2]] <- 1
    forPlot[labForMatr[[i]][2],labForMatr[[i]][1]] <- 1 
}

Осуществляем на основании финальной матрицы многомерное шкалирование и готовим массив fpts для визуализации.

distanciya <- dist(forPlot)
fit <- cmdscale(distanciya,eig=TRUE, k=2)
fit # view results
fpts <- as.data.frame(fit$points)
fpts$V1 <- fpts$V1 * -1
fpts$V3 <- row.names(forPlot)

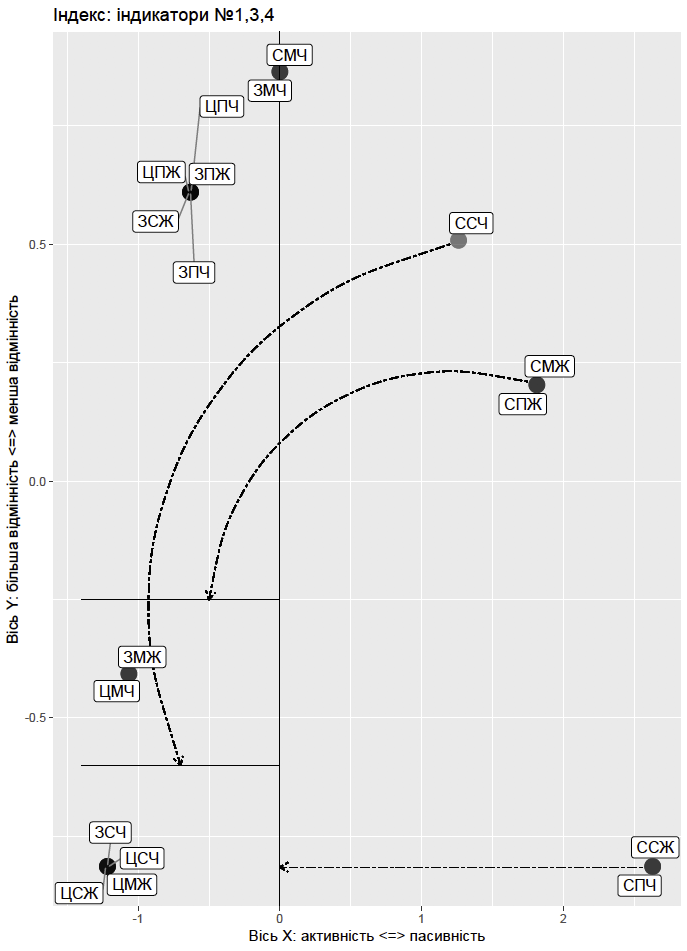
Строим диаграмму (см. рис. ниже) на основании результатов многомерного шкалирования, где точки представляют различные соц-дем группы (понадобятся библиотеки ggplot2 и ggrepel). Делим ее на сектора, позволяющие осуществить интерпретацию различий. Одна вертикальная линия проходит через 0 по оси Y и пересекает координату групп, которые вообще не показали статистически значимых отличий с другими. На диаграмме это молодые мужчины на юго-востоке (СМЧ) и молодые мужчины на западе (ЗМЧ). В свою очередь для демонстрации статистически значимых различий использованы стрелки. Если стрелка уходит от определенной координаты к вертикальной линии, то соответствующая демографическая(-ие) группа(-ы) является статистически отличной(-ыми) от всех групп, находящихся слева от этой линии. Если же стрелка идет к горизонтальной линии, то соответствующая демографическая(-ие) группа(-ы) являются статистически отличной(-ыми) от всех групп, находящихся ниже этой линии.

par(mar=c(2.5,7,2,1))

p <- ggplot(data = fpts, aes(x = V1, y = V2, label=V3))


pfin <- p + geom_point(size = 5, colour = "black", alpha = 0.5) + 
    ggtitle("Індекс: індикатори №1,3,4") + xlab("Вісь Х: активність <=> пасивність") + 
    ylab("Вісь Y: більша відмінність <=> менша відмінність")
    
pfin <- pfin + geom_errorbarh(aes(y=-0.25, xmin=-1.4, xmax=0, height = 0)) +
    geom_errorbarh(aes(y=-0.6, xmin=-1.4, xmax=0, height = 0)) +
    geom_vline(aes(xintercept=0)) +
    geom_curve(aes(x = 1.2, y = 0.5, xend = -0.7, yend = -0.6), linetype="twodash", 
               arrow = arrow(length = unit(0.015, "npc"))) +
    geom_curve(aes(x = 1.75, y = 0.21, xend = -0.5, yend = -0.25), linetype="twodash", 
               arrow = arrow(length = unit(0.015, "npc"))) +
    geom_segment(aes(x = 2.56, y = -0.815, xend = 0, yend = -0.815), linetype="twodash", 
                 arrow = arrow(length = unit(0.015, "npc")))
pfin + 
    geom_label_repel(aes(label = V3),
                     box.padding   = 0.1, 
                     point.padding = 0.2,
                     segment.color = 'grey50',
                     size = 4)