Статистические выводы: таблицы сопряженности и сравнение средних
20/08/14 23:43 Относится к категории: Анализ данных | R

В предыдущих двух главах было рассмотрено построение частотных таблиц (в том числе и таблиц сопряженности), а также средних значений, как методы описательной статистики. Как известно эти методы позволяют делать и статистические выводы. Последним и посвящена эта глава.
В случае таблиц сопряженности предварительно необходимо создать соответствующие объекты и уже к ним применять статистические критерии. В случае же сравнения средних значений работа может вестись как с массивом данных напрямую, так и со специально созданными векторами.
Таблицы сопряженности
Построим таблицу, связывающую тип избирательной системы и статус сободы в стране (поскольку при расчете хи-квадрат используются частоты, не будем рассчитывать проценты или пропорции):
Построим таблицу, связывающую тип избирательной системы и статус сободы в стране (поскольку при расчете хи-квадрат используются частоты, не будем рассчитывать проценты или пропорции):
1 2 3 4 5 6 7 | > someTable <- table(forT$freedom, forT$election)
> someTable
Мажоритарная Смешанная Пропорциональная
свободная 28 11 46
частично свободная 18 18 21
несвободная 23 10 8
|
На самом деле массив сплошной, т.е. в нем присутствуют данные про все (ну или почти все) единицы генеральной совокупности. Но в дидактических целях мы будем считать это исследование выборочным. Как видно из полученных результатов, есть определенная тенденция. Теперь проверим ее с помощью критерия независимости хи-квадрат с помощью функции chisq.test(), принимающая в качестве аргумента объект-таблицу:
8 9 10 11 12 13 | > chisq.test(someTable) Pearson's Chi-squared test data: someTable X-squared = 18.9821, df = 4, p-value = 0.0007923 |
Результаты более чем однозначные. Теперь для полноты картины можно взглянуть и на распределение соответствующих процентных величин:
14 15 16 17 18 19 | > round(prop.table(someTable,2),3)*100
Мажоритарная Смешанная Пропорциональная
свободная 40.6 28.2 61.3
частично свободная 26.1 46.2 28.0
несвободная 33.3 25.6 10.7
|
Кроме определения статистической значимости связи часто необходимо определить и ее силу. Для расчета соответствующих коэффициентов следует использовать функцию assocstats() библиотеки "vcd":
20 21 22 23 24 25 26 27 28 29 30 | > install.packages("vcd")
> library(grid) # эта библиотека также может понадобиться
> library(vcd)
> assocstats(someTable)
X^2 df P(> X^2)
Likelihood Ratio 19.437 4 0.00064480
Pearson 18.982 4 0.00079233
Phi-Coefficient : 0.322
Contingency Coeff.: 0.307
Cramer's V : 0.228
|
Как видно в результате получены данные как для статистической значимости (X^2, df и p), так и три коэффициента связи.
Средние значения
Для сравнения средних с помощью t-критерия Стьюдента для независимых групп используется функция t.test(), принимающая в качестве агрументов:
Для сравнения средних с помощью t-критерия Стьюдента для независимых групп используется функция t.test(), принимающая в качестве агрументов:
- группы сравниваемых данных;
- равенство/неравенство дисперсий;
- односторонний/двусторонний критерий сравнения.
Группы сравниваемых данных могут быть заданы двумя способами: а) с помощью формулы вида "y ~ x", в которой y является зависимой непрерывной, а x - независимой дихотомической переменной (при этом в виде дополнительного параметра необходимо указать фрейм данных, к которому имеет отношение эта формула); б) два числовых вектора, которые необходимо сравнить.
Равенство/неравенство дисперсий задается с помощью логического аргумента var.eual.
Тип критерия определяется с помощью аргумента alternative (возможные значения - less, greater, two.sided).
Если необходимо сделать доверительный уровень отличным от 95%, используется аргумент conf.level (указывается соответствующая пропорция)
Рассмотрим пример (первый способ определения сравниваемых групп):
Равенство/неравенство дисперсий задается с помощью логического аргумента var.eual.
Тип критерия определяется с помощью аргумента alternative (возможные значения - less, greater, two.sided).
Если необходимо сделать доверительный уровень отличным от 95%, используется аргумент conf.level (указывается соответствующая пропорция)
Рассмотрим пример (первый способ определения сравниваемых групп):
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | > forT$freedomTwo <- NA
> forT$freedomTwo[forT$freedom == "свободная"] <- "свободная"
> forT$freedomTwo[forT$freedom == "частично свободная" | forT$freedom == "несвободная"] <- "несвободная"
> var(forT$health[forT$freedomTwo == "свободная"],na.rm=T)
[1] 47.10881
> var(forT$health[forT$freedomTwo == "несвободная"],na.rm=T)
[1] 90.05752
> t.test(health ~ freedomTwo,
+ data = forT,
+ var.equal = F
+ )
Welch Two Sample t-test
data: health by freedomTwo
t = -8.0522, df = 186.753, p-value = 9.296e-14
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-11.858159 -7.191167
sample estimates:
mean in group несвободная mean in group свободная
65.79143 75.31609
|
В строках с 31 по 37 даны команды для подготовки данных и проверки величины дисперсий для сравниваемых групп.
Поскольку в функции t.test() явно не заданы такие аргументы как тип критерия и доверительный уровень, то соответствующие показатели принимаются за двусторонний (two.sided) и 95% (0.95) соответственно. В строках 46 и 47 видно, что различия являются статистически значимыми - в свободных странах ожидаемая продолжительность жизни в среднем на 10 лет больше, чем в остальных.
Теперь рассмотрим второй способ:
Поскольку в функции t.test() явно не заданы такие аргументы как тип критерия и доверительный уровень, то соответствующие показатели принимаются за двусторонний (two.sided) и 95% (0.95) соответственно. В строках 46 и 47 видно, что различия являются статистически значимыми - в свободных странах ожидаемая продолжительность жизни в среднем на 10 лет больше, чем в остальных.
Теперь рассмотрим второй способ:
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | > firstG <- forT$income[forT$freedom == "свободная"] > secondG <- forT$income[forT$freedom == "частично свободная" | forT$freedom == "несвободная"] > var(firstG, na.rm=T) [1] 153805145 > var(secondG, na.rm=T) [1] 175370303 > t.test(firstG, secondG, + var.equal = F, + conf.level = 0.99) Welch Two Sample t-test data: firstG and secondG t = 5.121, df = 176.492, p-value = 7.903e-07 alternative hypothesis: true difference in means is not equal to 0 99 percent confidence interval: 4776.631 14660.005 sample estimates: mean of x mean of y 17861.99 8143.67 |
Использование R Commander-а
Если работать через диалоговые окна, то процесс будет иметь следующий вид.
Сначала выбираем нужную базу данных (кнопка напротив Data set):
Если работать через диалоговые окна, то процесс будет иметь следующий вид.
Сначала выбираем нужную базу данных (кнопка напротив Data set):
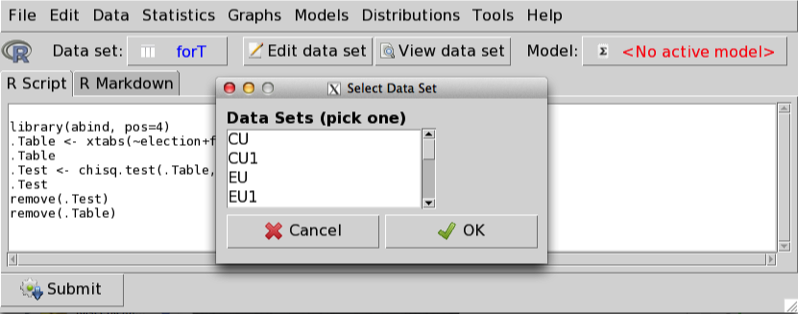
Далее для таблиц сопряженности:
1.
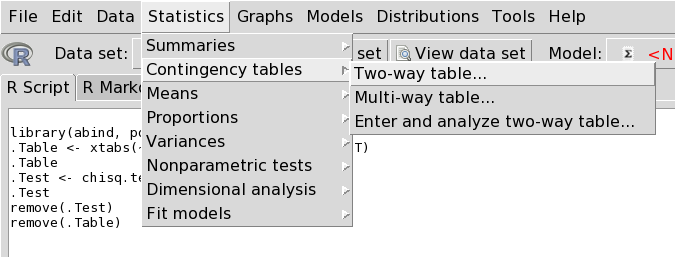
2.
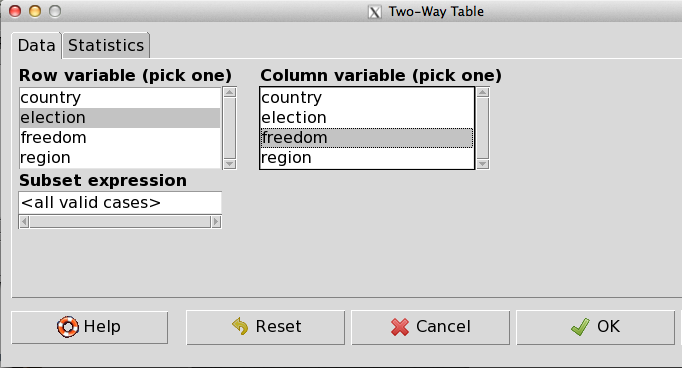
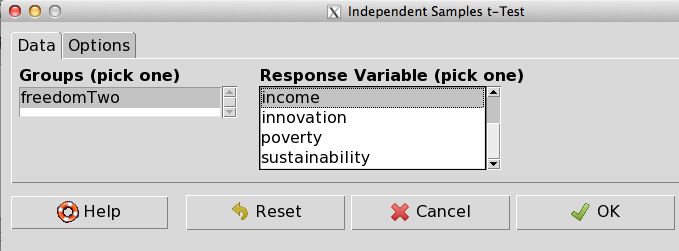
Для сравнения средних (предварительно надо убедиться, что группирующая переменная имеет две категории и является переменной-фактором):
1.
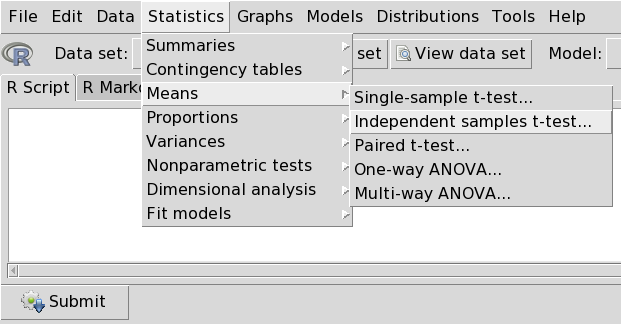
2.
статью подготовил кандидат социологических наук Сергей Дембицкий
Вверх
blog comments powered by Disqus