Критерий Шапиро-Уилка: выборки и статистическая значимость
21/01/16 18:51 Относится к категории: Анализ данных | R | Шкалирование | Эмпирическая социология | Психологический дистресс
В процессе написания статьи, посвященной сокращенному варианту SCL-90-R (SCL-9-NR), столкнулся с проверкой распределения на нормальность посредством критерия Шапиро-Уилка. Проверялось это дело на двух выборках - для Киева и Львова (по 200 человек в каждой). Пришлось прибегнуть к некоторым ухищрениям. Вот собственно о них кратенько в этой заметке.
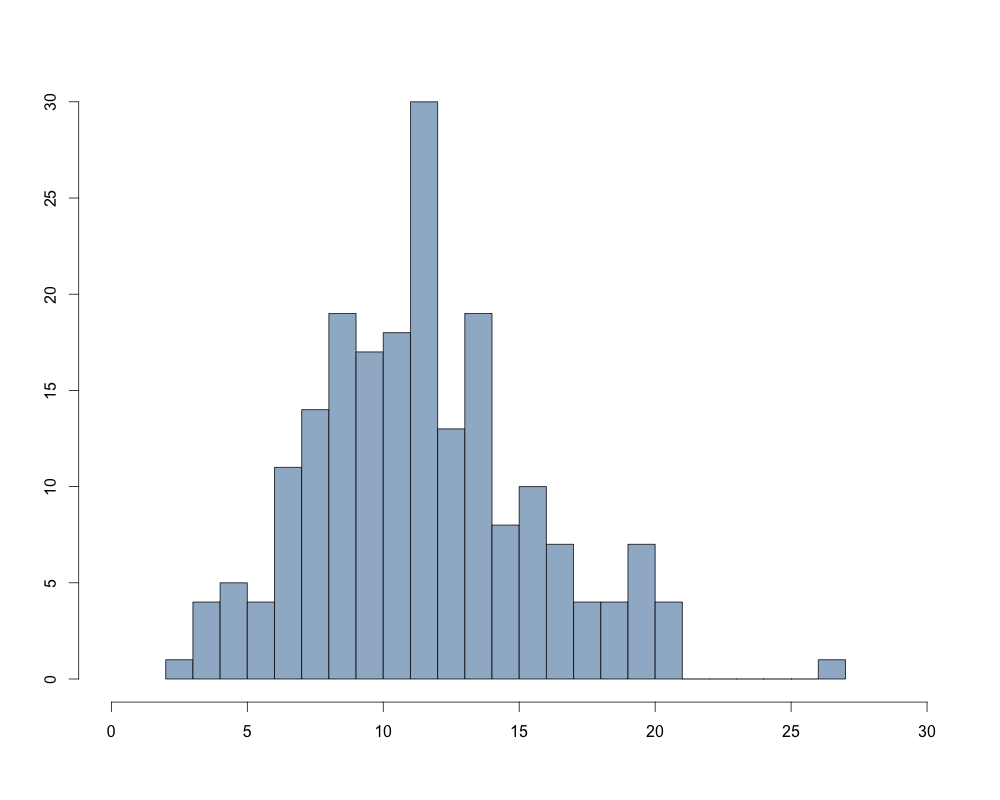
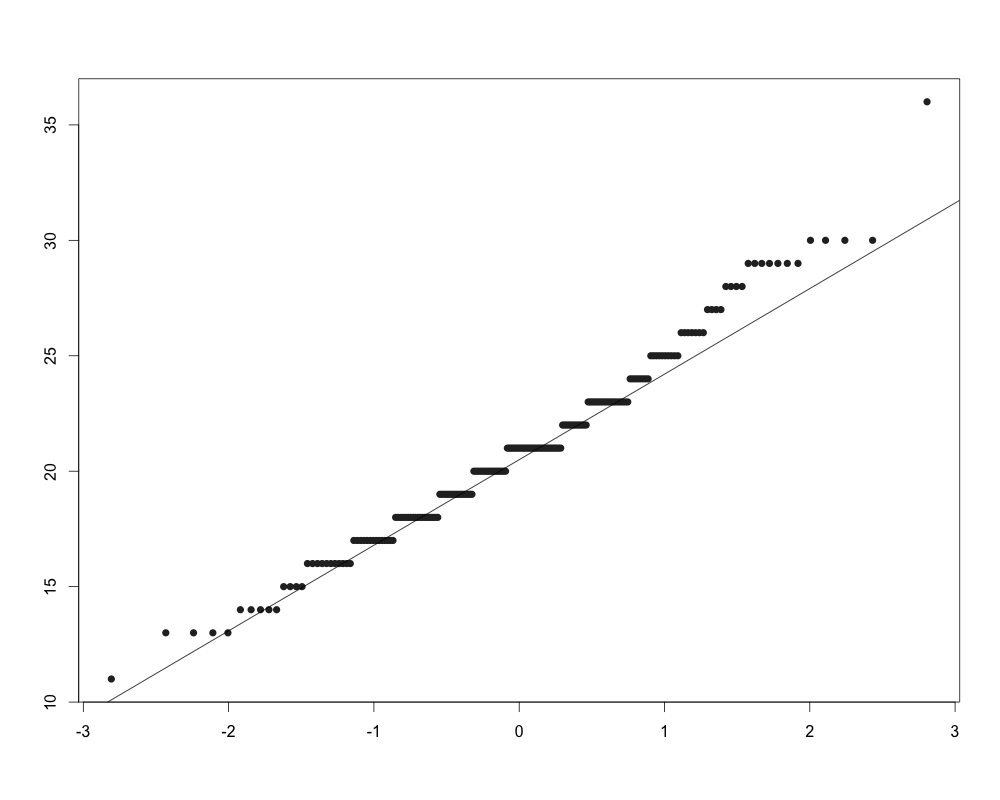


Киев


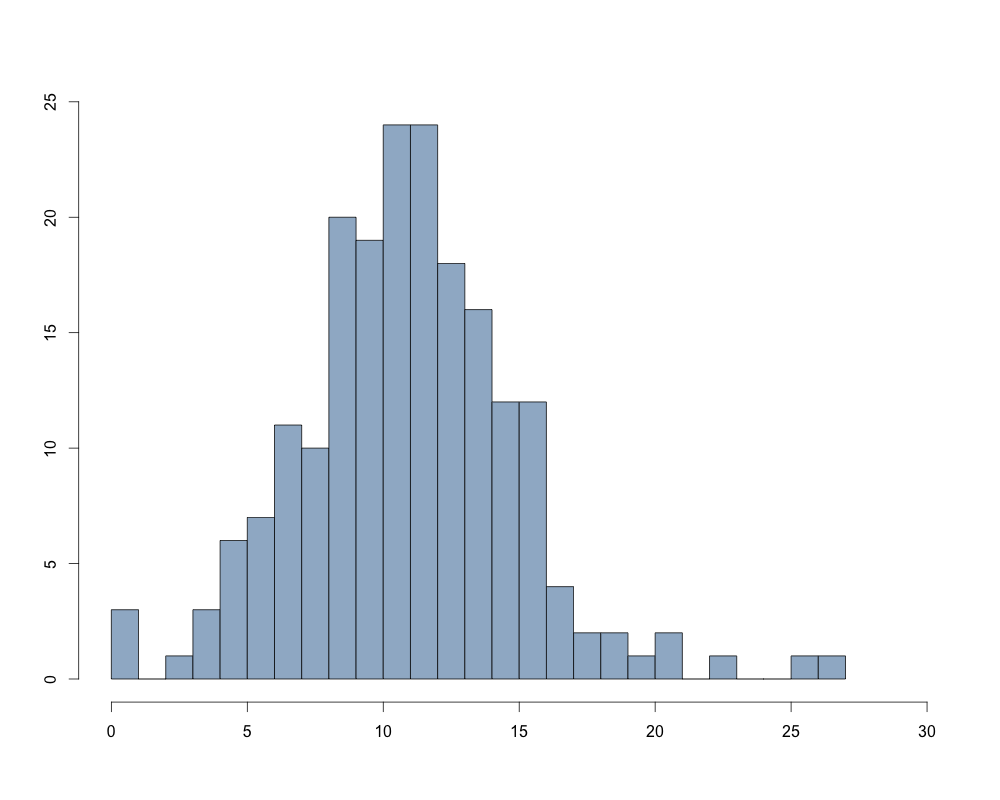
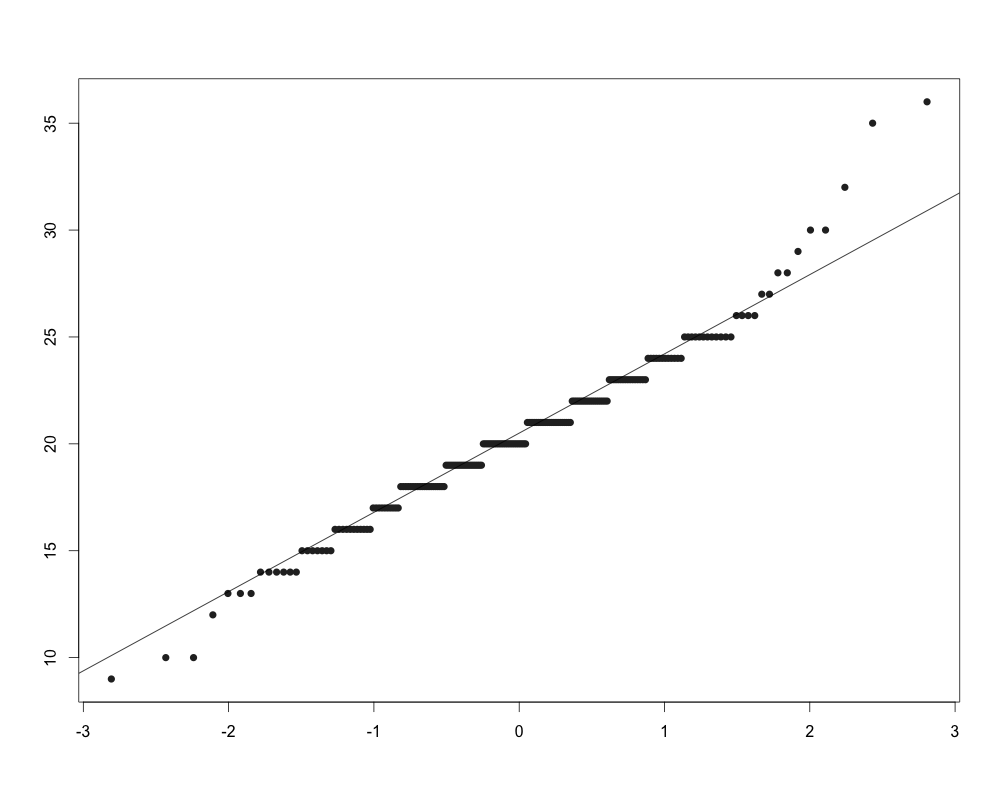
Львов
Распределение значений SCL-9-NR в обоих исследованиях визуально напоминает нормальное. Графики квантилей показывают отклонение от нормальности для высоких значений индекса. При этом результаты теста Шапиро-Уилка указывают на то, что распределение статистически значимо отлично от нормального как для исследования в Киеве (W = 0,98; p < 0,01), так и для исследования во Львове (W = 0,97; p < 0,01). Вместе с тем, этот критерий очень чувствителен к размеру выборки – чем больше выборка, тем выше вероятность отклонения нулевой гипотезы.
Чтобы проверить влияние размера выборки на результаты теста в моем случае, я сформировал случайные выборки размером 100, 50 и 25 наблюдений 1000 раз для каждого из двух исследований на основании их собственных массивов. Для каждой выборки был использован критерий Шапиро-Уилка, что позволило определить количество случаев, в которых принимается нулевая гипотеза (n[p > 0,05]), и среднюю вероятность случайной ошибки для выборок различного размера (Xp). На основании этих показателей можно оценить соответствия распределений нормальному:
Как видно на выборке в 25 наблюдений нулевая гипотеза подтвердилась в 87,5% случаев для киевского исследования и 78,2% - для львовского. Средняя же вероятность получения распределения отличного от нормального вследствие случайности выросла практически до 40%, что существенно выше требуемых 5%.
С помощью R это делается очень просто. Например:
testShapiro <- c()
for (i in 1:1000) testShapiro[i] <- shapiro.test(sample(distresLvov$scl9nr-9, 100))[2]
testND <- sapply(testShapiro, function(x) x > 0.05)
sum(testND)
sum(unlist(testShapiro)) / 1000
Чтобы проверить влияние размера выборки на результаты теста в моем случае, я сформировал случайные выборки размером 100, 50 и 25 наблюдений 1000 раз для каждого из двух исследований на основании их собственных массивов. Для каждой выборки был использован критерий Шапиро-Уилка, что позволило определить количество случаев, в которых принимается нулевая гипотеза (n[p > 0,05]), и среднюю вероятность случайной ошибки для выборок различного размера (Xp). На основании этих показателей можно оценить соответствия распределений нормальному:
| Размер выборки | Киев | Львов | ||
| n[p > 0,05] | Xp | n[p > 0,05] | Xp | |
| 100 | 467 | 0.08 | 349 | 0.09 |
| 50 | 764 | 0.25 | 659 | 0.23 |
| 25 | 875 | 0.37 | 782 | 0.36 |
Как видно на выборке в 25 наблюдений нулевая гипотеза подтвердилась в 87,5% случаев для киевского исследования и 78,2% - для львовского. Средняя же вероятность получения распределения отличного от нормального вследствие случайности выросла практически до 40%, что существенно выше требуемых 5%.
С помощью R это делается очень просто. Например:
testShapiro <- c()
for (i in 1:1000) testShapiro[i] <- shapiro.test(sample(distresLvov$scl9nr-9, 100))[2]
testND <- sapply(testShapiro, function(x) x > 0.05)
sum(testND)
sum(unlist(testShapiro)) / 1000
blog comments powered by Disqus